
【题目】解答题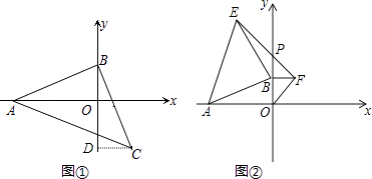
(1)如图①,等腰直角△ABC中,∠ABC=90°,AB=BC,点A、B分别在坐标轴上,若点C的横坐标为2,直接写出点B的坐标;(提示:过C作CD⊥y轴于点D,利用全等三角形求出OB即可)
(2)如图②,若点A的坐标为(﹣6,0),点B在y轴的正半轴上运动时,分别以OB、AB为边在第一、第二象限作等腰直角△OBF,等腰直角△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值.若变化,求PB的取值范围.
【答案】
(1)(0,2)
(2)
解:PB的长度不发生改变,
理由:如图3,作EG⊥y轴于G,
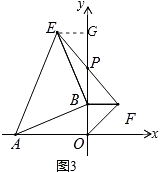
∵∠BAO+∠OBA=90°,∠OBA+∠EBG=90°,
∴∠BAO=∠EBG,
在△BAO和△EBG中, 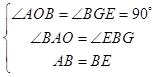
∴△BAO≌△EBG(AAS),
∴BG=AO,EG=OB,
∵OB=BF,
∴BF=EG,
在△EGP和△FBP中, 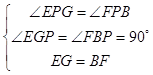 ,
,
∴△EGP≌△FBP(AAS),
∴PB=PG,
∴PB= ![]() BG=
BG= ![]() AO=3
AO=3
即:PB的长度不发生改变,是定值为3.
【解析】解:(1)如图1,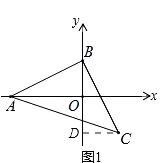
作CD⊥BO于D,
∵∠CBD+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠CBD=∠BAO,
在△ABO和△BCD中, ,
,
∴△ABO≌△BCD(AAS),
∴CD=BO=2,
∴B点坐标(0,2);
所以答案是:(0,2);


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°. 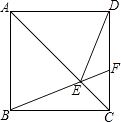
(1)∠ACB的大小=(度);
(2)求证:△ABE≌△ADE;
(3)∠AED的大小=(度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抛物线y=x2﹣4x+m的图象上有三个点(﹣3,y1),(1,y2),(4,y3),则y1,y2,y3的大小关系为( )
A.y2<y3<y1B.y1<y2=y3C.y1<y2<y3D.y3<y2<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为
A.(2,-3)B.(-2,-3)C.(-2,3) D. (-3,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.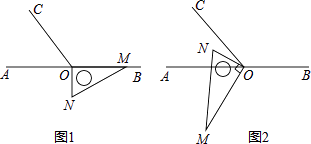
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
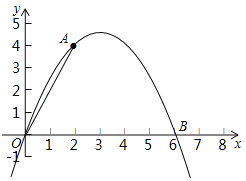
【题目】如图,二次函数![]() 的图象经过点A(2,4)与B(6,0).
的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组决定去市场购买A,B,C三种仪器,其单价分别为3元,5元,7元,购买这批仪器需花62元;经过讨价还价,最后以每种单价各下降1元成交,结果只花50元就买下了这批仪器.那么A种仪器最多可买( )
A.8件 B.7件 C.6件 D.5件
查看答案和解析>>
科目:初中数学 来源: 题型:
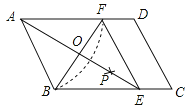
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是 ;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 ,∠ABC= °.(直接填写结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com