
【题目】如图,在平面直角坐标系中,![]() 坐标分别是
坐标分别是![]() ,且
,且![]() 满足
满足![]() ,现同时将点
,现同时将点![]() 分别向下平移3个单位,再向左平移1个单位,分别得到点
分别向下平移3个单位,再向左平移1个单位,分别得到点![]() 的对应点
的对应点![]() ,连接
,连接![]() .
.
(1)求点![]() 的坐标及四边形
的坐标及四边形![]() 的面积
的面积![]() ;
;
(2)在y轴上是否存在一点![]() ,连接
,连接![]() ,使
,使![]() ?若存在这样的点,求出点M的坐标,若不存在,试说明理由.
?若存在这样的点,求出点M的坐标,若不存在,试说明理由.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作: 将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )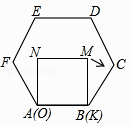
A.1.4
B.1.1
C.0.8
D.0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 ![]() 于点P,Q,且点P,Q在AB异侧,连接OP.
于点P,Q,且点P,Q在AB异侧,连接OP. 
(1)求证:AP=BQ;
(2)当BQ=4 ![]() 时,求
时,求 ![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,求OC的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC的垂直平分线分别交AB、BC于点D和点E,连接CD,AC=DC,∠B=25°,则∠ACD的度数是( )
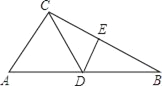
A. 50° B. 65° C. 80° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)求△ABC的面积为_______;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图,不写作法,保留作图痕迹.
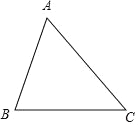
如图,△ABC中,∠A=60°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AB、BC两边的距离也相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ACP=15°,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC="70"o,求∠AGD。

解:∵EF∥AD,
∴∠2=∠3( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥DG ( )
∴∠BAC+ ="180"o( )
∵∠BAC=70 o,∴∠AGD= 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0)、B(4,﹣1)、C(3,2).
(1)在所给的直角坐标系中画出△ABC;
(2)把△ABC向左平移3个单位,再向上平移2个单位得到△A′B′C′,画出△A′B′C′并写出点C′的坐标;
(3)求△A′B′C′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com