解:(1)∵CD⊥AB,∴∠BDC=90°.
∵H是BC的中点,∴DH=BH=CH=

BC=1.
∴B(-1,0)、C(1,0).
又∵∠ABC=45゜,∴△BCD是等腰直角三角形,即y轴是BC的中垂线;
∴点D在y轴上,即D(0,1).
设过B、C、D三点的抛物线解析式为 y=a(x+1)(x-1),则有:
1=a(0+1)(0-1),解得 a=-1;
∴抛物线的解析式为 y=-x
2+1.
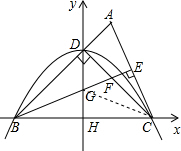
(2)线段BG与CE之间存在数量关系BG=

CE.
证明:连接CG.
∵H是BC的中点,DH⊥BC,∴CG=BG,∴∠GCB=∠GBC.
∵AB=BC,BE⊥AC,∴BE平分∠ABC.
又∵∠ABC=45゜,
∴∠GCB=∠BGC=22.5゜.
∴∠CGE=∠GCB+∠GBC=45゜.
∵BE⊥AC,
∴CG=
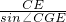
=
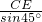
=

CE.
∴BG=

CE.
(3)不存在符合条件的点P,理由:
∵将△DHC平移、旋转、翻折(次数不限)后的三角形与△BDH能拼成特殊四边形,
∴拼成的特殊四边形除D、H、C三点外的第四个顶点的坐标只能是(1,1)或(-1,1)或(-1,-1).
经检验,点(1,1)、(-1,-1)、(-1,1)均不在(1)的抛物线y=-x
2+1上,故不存在符合条件的点P.
分析:(1)欲求抛物线的解析式,需明确B、C、D三点的坐标;已知BC的长,且H是BC的中点,则B、C的坐标可求.在Rt△BDC中,∠DBC=45゜,很显然该三角形是等腰直角三角形,则DH=BH=HC,由此求得点D的坐标,再利用待定系数法即可得出抛物线的解析式.
(2)由(1)知:△BDC是等腰直角三角形,即y轴正好是BC的垂直平分线,那么BG=GC,若连接GC,那么∠EGC=2∠EBC.由题意,在等腰△ABC中,BE⊥AC,显然BE是∠ABC的平分线,那么可得到的条件:∠EGC=∠ABC=45゜,在等腰Rt△EGC中,易得CG、CE的数量关系,而BG=GC,由此得解.
(3)若与△BDH拼成特殊四边形(面积不变),那么点P应该位于第一、二、三象限,且得到的特殊四边形为:正方形(BD、CD重合)、平行四边形(CH、BH重合或CH、HD重合),先求出这些点的坐标,然后代入抛物线中进行验证即可.
点评:该题涉及了二次函数解析式的确定,特殊三角形、特殊四边形的判定和性质等重点知识.在解题时,应注重数形结合的数学思想.

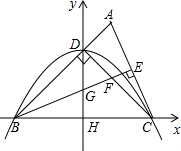 如图,△ABC中,AB=BC=2,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.以点H为原点,BC所在直线为x轴建立如图所示的平面直角坐标系.
如图,△ABC中,AB=BC=2,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.以点H为原点,BC所在直线为x轴建立如图所示的平面直角坐标系. CE吗?若存在,请证明;若不存在,请说明理由;
CE吗?若存在,请证明;若不存在,请说明理由; BC=1.
BC=1. (2)线段BG与CE之间存在数量关系BG=
(2)线段BG与CE之间存在数量关系BG= CE.
CE.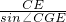 =
=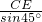 =
= CE.
CE. CE.
CE.

 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.