
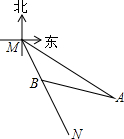
 如图,已知射线MN表示一艘轮船的航行路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为80海里.
如图,已知射线MN表示一艘轮船的航行路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为80海里.分析 (1)过A作AH⊥MN于H.由方向角的定义可知∠QMB=30°,∠QMA=60°,那么∠NMA=∠QMA-∠QMB=30°.解直角△AMH,得出AH=$\frac{1}{2}$AM=40海里,MH=$\sqrt{3}$AH=40$\sqrt{3}$海里;
(2)先根据直角三角形两锐角互余求出∠HAM=60°,由∠MAB=15°,得出∠HAB=∠HAM-∠MAB=45°,那么△AHB是等腰直角三角形,得出BH=AH=40海里.
解答 解:(1)如图,过A作AH⊥MN于H.
∵∠QMB=30°,∠QMA=60°,
∴∠NMA=∠QMA-∠QMB=30°.
在直角△AMH中,∵∠AHM=90°,∠AMH=30°,AM=80海里,
∴AH=$\frac{1}{2}$AM=40海里,MH=$\sqrt{3}$AH=40$\sqrt{3}$海里,
即点A到航线MN的距离为40海里;
(2)在直角△AMH中,∵∠AHM=90°,∠AMH=30°,
∴∠HAM=60°,
∵∠MAB=15°,
∴∠HAB=∠HAM-∠MAB=45°,
∵∠AHB=90°,
∴BH=AH=40海里,
∵MH=40$\sqrt{3}$海里,
∴MB=(40$\sqrt{3}$-40)海里.
点评 本题考查了解直角三角形的应用-方向角问题,含30°角的直角三角形的性质,等腰直角三角形的判定与性质,直角三角形两锐角互余的性质,准确作出辅助线构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
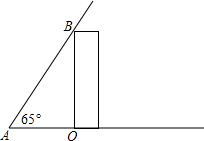 如图,为测量一幢大楼的高度,在地面上距离楼底O点30m的点A处,测得楼顶B点的仰角∠OAB=65°,则这幢大楼的高度为( )m.
如图,为测量一幢大楼的高度,在地面上距离楼底O点30m的点A处,测得楼顶B点的仰角∠OAB=65°,则这幢大楼的高度为( )m.| A. | 30•sin65° | B. | $\frac{30}{cos65°}$ | C. | 30•tan65° | D. | $\frac{30}{tan65°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com