
科目:初中数学 来源: 题型:填空题
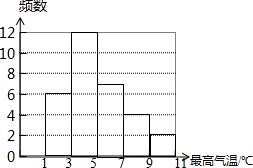 根据石家庄2014年1月份全月的各天最高气温(℃)记录,绘制出如图所示的频数分布直方图(图中分组含量低值,不含最高值),由图中信息可知,最高气温达到5℃及其以上的有13天.
根据石家庄2014年1月份全月的各天最高气温(℃)记录,绘制出如图所示的频数分布直方图(图中分组含量低值,不含最高值),由图中信息可知,最高气温达到5℃及其以上的有13天.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
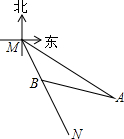 如图,已知射线MN表示一艘轮船的航行路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为80海里.
如图,已知射线MN表示一艘轮船的航行路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为80海里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com