
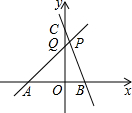 如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=-3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.若四边形PQOB的面积是5.5,且CQ:AO=1:2,若存在一点D,使以A、B、P、D为顶点的四边形是平行四边形,则点D的坐标为($\frac{13}{2}$,$\frac{9}{2}$)或(-$\frac{11}{2}$,$\frac{9}{2}$)或(-$\frac{5}{2}$,-$\frac{9}{2}$).
如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=-3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.若四边形PQOB的面积是5.5,且CQ:AO=1:2,若存在一点D,使以A、B、P、D为顶点的四边形是平行四边形,则点D的坐标为($\frac{13}{2}$,$\frac{9}{2}$)或(-$\frac{11}{2}$,$\frac{9}{2}$)或(-$\frac{5}{2}$,-$\frac{9}{2}$). 分析 已知直线解析式,令y=0,求出x的值,可求出点A,B的坐标.联立方程组求出点P的坐标;先根据CQ:AO=1:2得到m、n的关系,然后求出S△AOQ,S△PAB并都用字母m表示,根据S四边形PQOB=S△PAB-S△AOQ,列式求出m与n的值,得出点P的坐标;根据图形以A、B、P、D为顶点的四边形是平行四边形,如图所示,求出满足题意D1,D2,D3的坐标.
解答 解:在直线y=x+m中,令y=0,得x=-m,
∴点A(-m,0),
在直线y=-3x+n中,令y=0,得x=$\frac{n}{3}$,
∴点B($\frac{n}{3}$,0),
由$\left\{\begin{array}{l}{y=x+m}\\{y=-3x+n}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{n-m}{4}}\\{y=\frac{n+3m}{4}}\end{array}\right.$,
∴点P($\frac{n-m}{4}$,$\frac{n+3m}{4}$),
∵CQ:AO=1:2,
∴(n-m):m=1:2,
整理得3m=2n,
∴n=$\frac{3}{2}$m,
∴$\frac{n+3m}{4}$=$\frac{\frac{3}{2}m+3m}{4}$=$\frac{9}{8}$m,
由题意得:S四边形PQOB=S△PAB-S△AOQ=$\frac{1}{2}$($\frac{n}{3}$+m)×($\frac{9}{8}$m)-$\frac{1}{2}$×m×m=$\frac{11}{32}$m2=5.5,
解得:m=±4,
∵m>0,
∴m=4,
∴n=$\frac{3}{2}$m=6,
∴P($\frac{1}{2}$,$\frac{9}{2}$),
存在一点D,使以A、B、P、D为顶点的四边形是平行四边形,
过点P作直线PM平行于x轴,过点B作AP的平行线交PM于点D1,过点A作BP的平行线交PM于点D2,过点A、B分别作BP、AP的平行线交于点D3.
①∵PD1∥AB且BD1∥AP,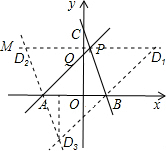
∴PABD1是平行四边形.此时PD1=AB,易得D1($\frac{13}{2}$,$\frac{9}{2}$);
②∵PD2∥AB且AD2∥BP,
∴PBAD2是平行四边形.此时PD2=AB,易得D2(-$\frac{11}{2}$,$\frac{9}{2}$);
③∵BD3∥AP且AD3∥BP,此时BPAD3是平行四边形.
∵BD3∥AP且B(2,O),
∴yBD3=x-2.同理可得yAD3=-3x-12,
联立得:$\left\{\begin{array}{l}{y=x-2}\\{y=-3x-12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-\frac{5}{2}}\\{y=-\frac{9}{2}}\end{array}\right.$,
∴D3(-$\frac{5}{2}$,-$\frac{9}{2}$).
故答案为:($\frac{13}{2}$,$\frac{9}{2}$)或(-$\frac{11}{2}$,$\frac{9}{2}$)或(-$\frac{5}{2}$,-$\frac{9}{2}$)
点评 此题属于一次函数综合题,涉及的知识有:一次函数图象的交点,坐标与图形性质,平行四边形的判定与性质,一次函数与坐标轴的交点,熟练掌握一次函数的性质是解本题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:选择题
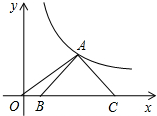 如图,等腰Rt△ABC的底边BC在x轴上,顶点A在双曲线y=$\frac{3}{x}$(x>0)上,连接OA,则OC2-OA2=( )
如图,等腰Rt△ABC的底边BC在x轴上,顶点A在双曲线y=$\frac{3}{x}$(x>0)上,连接OA,则OC2-OA2=( )| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | -2+$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com