
如图,已知△OAB的顶点A(-6,0),B(0,2),O是坐标原点, 将△OAB绕点O按顺时针旋转90°,得到△ODC.

(1)写出C点的坐标为 ;
(2)设过A,D,C三点的抛物线的解析式为 ,求其解析式?
,求其解析式?
(3)证明AB⊥BE.
(1)C(2,0),D(0,6);(2)y=﹣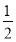 x2﹣2x+6;(3)证明见解析.
x2﹣2x+6;(3)证明见解析.
【解析】
试题分析:(1)根据旋转的性质,可得OC=OB,OD=OA,进而可得C、D两点的坐标;
(2)由于抛物线过点A(﹣6,0),C(2,0),所以设抛物线的解析式为y=a(x+6)(x﹣2)(a≠0),再将D(0,6)代入,求出a的值,得出抛物线的解析式,然后利用配方法求出顶点E的坐标;
(3)已知A、B、E三点的坐标,运用两点间的距离公式计算得出AB2=40,BE2=40,AE2=80,则AB2+BE2=AE2,根据勾股定理的逆定理即可证明AB⊥BE.
试题解析:(1)∵将△OAB绕点O按顺时针旋转90°,得到△ODC,
∴△ODC≌△OAB,
∴OC=OB=2,OD=OA=6,
∴C(2,0),D(0,6);
(2)∵抛物线过点A(﹣6,0),C(2,0),
∴可设抛物线的解析式为y=a(x+6)(x﹣2)(a≠0),
∵D(0,6)在抛物线上,
∴6=﹣12a,
解得a=﹣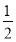 ,
,
∴抛物线的解析式为y=﹣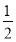 (x+6)(x﹣2),即y=﹣
(x+6)(x﹣2),即y=﹣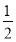 x2﹣2x+6;
x2﹣2x+6;
(3)∵y=﹣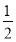 x2﹣2x+6=﹣
x2﹣2x+6=﹣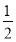 (x+2)2+8,
(x+2)2+8,
∴顶点E的坐标为(﹣2,8),
连接AE.
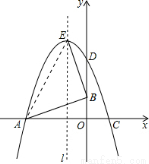
∵A(﹣6,0),B(0,2),E(﹣2,8),
∴AB2=62+22=40,BE2=(﹣2﹣0)2+(8﹣2)2=40,AE2=(﹣2+6)2+(8﹣0)2=80,
∴AB2+BE2=AE2,
∴AB⊥BE..
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年广东省九年级下册期末检测数学试卷(解析版) 题型:解答题
已知三角形两边长分别是3和4,第三边长是方程x2–6x+5=0的根,试判断这个三角形的形状。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省中考预测二数学试卷(解析版) 题型:选择题
如图,点A的坐标为(- ,0),点B在直线y=x上运动,当线段AB最短时点B的坐为( )
,0),点B在直线y=x上运动,当线段AB最短时点B的坐为( )

A.(- ,-
,- ) B.(-
) B.(- ,-
,- )
)
C.( ,-
,- ) D.(0,0)
) D.(0,0)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东汕头市九年级下学期第一次阶段考试数学试卷(解析版) 题型:选择题
如图,在梯形ABCD中,AD∥BC,AD=2,AB=3,BC=6,沿AE翻折梯形ABCD使点B落AD的延长线上,记为点B’,连结B’E交CD于点F,则 的值为( )
的值为( )

A. B.
B. C.
C.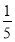 D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东青岛平度古岘镇古岘中学九年级下学期阶段性质量检测数学试卷(解析版) 题型:解答题
为了把青岛市建成国家级文明城市,加强行人交通管理。特在每个红绿灯处设置了文明监督岗,文明劝导员老张某天在香港中路的一十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段(以1小时为一个时间段),对闯红灯的人数制作了如图所示的扇形统计图和条形统计图,但均不完整.请你根据统计图解答下列问题:

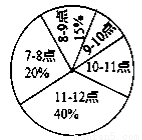
(1)问这一天上午7:00~12:00这一时间段共有多少人闯红灯?
(2)请你把条形统计图补充完整;
(3)求这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数和中位数.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省淄博市桓台县九年级中考模拟数学试卷(解析版) 题型:解答题
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数 的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数y=kx+3-3k(k≠0)的图象一定过点C;
(3)对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com