
【题目】某中学在艺术节期间向全校学生征集书画作品,美术王老师从全校随机抽取了四个班级记作A、B、C、D,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
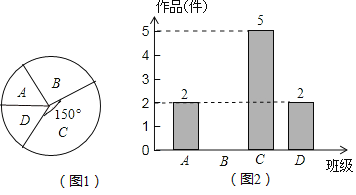
(1)王老师抽查的四个班级共征集到作品多少件?
(2)请把图2的条形统计图补充完整;
(3)若全校参展作品中有五名同学获得一等奖,其中有三名男生、二名女生.现在要在其中抽两名同学去参加学校总结表彰座谈会,请用画树状图或列表的方法求恰好抽中一名男生一名女生的概率.
科目:初中数学 来源: 题型:
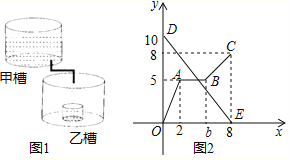
【题目】图1是甲、乙两个圆柱形水槽,一个圆柱形的空玻璃杯放置在乙槽中(空玻璃杯的厚度忽略不计).将甲槽的水匀速注入乙槽的空玻璃杯中,甲水槽内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2线段DE所示,乙水槽(包括空玻璃杯)内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2折线O﹣A﹣B﹣C所示.记甲槽底面积为S1,乙槽底面积为S2,乙槽中玻璃杯底面积为S3,则S1:S2:S3的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠ACB=∠EFD=90,△DEF,的顶点E与△ABC的斜边AB的中点重合.将△DEF绕点E旋转,旋转过程中,线段AC与线段EF相交于点Q,射线ED与射线BC相交于点P.
(1)求证:△AEQ∽△BPE;
(2)求证:PE平分∠BPQ;
(3)当AQ=2,AE=![]() ,求PQ的长.
,求PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.三角形的外心到三角形的三个顶点的距离相等
B.如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16
C.将一次函数y=3x-1的图象向上平移3个单位,所得直线不经过第四象限
D.若关于x的一元一次不等式组![]() 无解,则m的取值范围是
无解,则m的取值范围是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
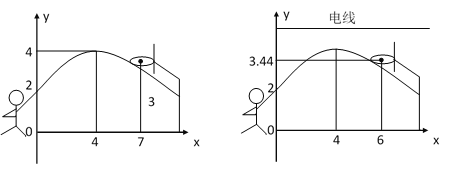
【题目】在小明的一次投篮中,球出手时离地面高2米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米.篮球运行的轨迹为抛物线,篮球中心距离地面3米,通过计算说明此球能否投中.
探究一:若出手的角度、力度和高度都不变的情况下,求小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮筐中?
探究二:若出手的角度、力度和高度都发生改变的情况下,但是抛物线的顶点等其他条件不变,求小明出手的高度需要增加多少米才能将篮球投入篮筐中?
探究三:若出手的角度、力度都改变,出手高度不变,篮筐的坐标为(6,3.44),球场上方有一组高6米的电线,要想在篮球不触碰电线的情况下,将篮球投入篮筐中,直接写出二次函数解析式中a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
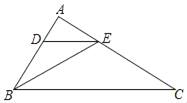
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,AE2=ADAB,∠ABE=∠ACB.
(1)求证:DE∥BC;
(2)如果S△ADE:S四边形DBCE=1:8,求S△ADE:S△BDE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com