
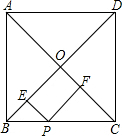
 如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 先根据勾股定理求出对角线BD,证明△BEP是等腰直角三角形,得出PE=BE,再证明四边形OEPF是矩形,得出PF=OE,得出PE+PF=BE+OE=OB即可.
解答 解:∵四边形ABCD是正方形,
∴AB=AD=1,AC⊥BD,∠ABC=∠BCD=90°,∠CBO=∠BCO=45°,OB=$\frac{1}{2}$BD,
∴BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,∠BOC=90°,
∴OB=$\frac{\sqrt{2}}{2}$,
∵PE⊥BD于点E,PF⊥AC于点F,
∴∠OEP=∠OFP=90°=∠EOF,△BEP是等腰直角三角形,
∴四边形OEPF是矩形,PE=BE,
∴PF=OE,
∴PE+PF=BE+OE=OB=$\frac{\sqrt{2}}{2}$;
故选:B.
点评 本题考查了正方形的性质、勾股定理、等腰直角三角形的判定与性质、矩形的判定;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源:2016-2017学年四川达县万家中学下学期九年级第一次月考数学试卷(解析版) 题型:单选题
某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是 ( )
A. (3+x)(4﹣0.5x)=15 B. (x+3)(4+0.5x)=15
C. (x+4)(3﹣0.5x)=15 D. (x+1)(4﹣0.5x)=15
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:选择题
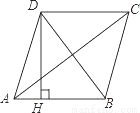
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A.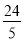 B.
B.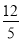 C.5 D.4
C.5 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
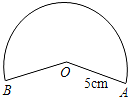 小明用图中所示的扇形纸片作一个圆锥的侧面,小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )
小明用图中所示的扇形纸片作一个圆锥的侧面,小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 2cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查全国中学生心理健康现状 | |
| B. | 调查你所在的班级同学的身高情况 | |
| C. | 调查我市食品合格情况 | |
| D. | 调查苏州电视台《新闻夜班车》的收视率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com