
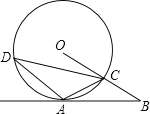
【题目】已知:如图A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,∠B=30°.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CE是⊙O切线,C是切点,EA交弦BC于点D、交⊙O于点F,连接CF:
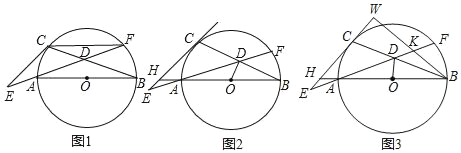
(1)如图1,求证:∠ECB=∠F+90°;
(2)如图2,连接CD,延长BA交CE于点H,当OD⊥BC、HA=HE时,求证:AB=CE;
(3)如图3,在(2)的条件K在EF上,EH=![]() FK,S△ADO=
FK,S△ADO=![]() ,求WE的长.
,求WE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(﹣1,0),点B(0,﹣2),AD与y轴交于点E,且E为AD的中点,双曲线y=![]() 经过C,D两点且D(a,4)、C(2,b).
经过C,D两点且D(a,4)、C(2,b).
(1)求a、b、k的值;
(2)如图2,线段CD能通过旋转一定角度后点C、D的对应点C′、D′还能落在y=![]() 的图象上吗?如果能,写出你是如何旋转的,如果不能,请说明理由;
的图象上吗?如果能,写出你是如何旋转的,如果不能,请说明理由;
(3)如图3,点P在双曲线y=![]() 上,点Q在y轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试求满足要求的所有点P、Q的坐标.
上,点Q在y轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试求满足要求的所有点P、Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=30°,P为AB中点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.
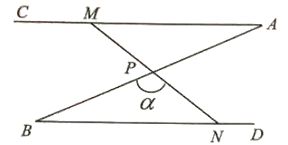
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
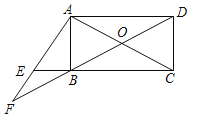
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动,如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:
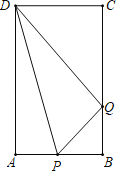
(1)当运动开始后1秒时,求△DPQ的面积;
(2)当运动开始后![]() 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;
(3)在运动过程中,存在这样的时刻,使△DPQ以PD为底的等腰三角形,求出运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(a)、图(b)、图(c)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在下图中分别画出符合要求的图形,所画图形各顶点必须在方格纸的格点上.

(1)在图(a)中画一个等腰三角形,使它的底边长是4,且面积是16;
(2)在图(b)中画一个等腰直角三角形,使它的面积是10;
(3)在图(c)中画一个四边形,使它既是轴对称又是中心对称图形,且面积是29.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() =
= ![]() =
=![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②请直接写出线段AD,BD,CD之间的等量关系式;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com