
【题目】如图,AB是⊙O的直径,CE是⊙O切线,C是切点,EA交弦BC于点D、交⊙O于点F,连接CF:
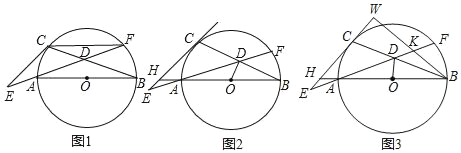
(1)如图1,求证:∠ECB=∠F+90°;
(2)如图2,连接CD,延长BA交CE于点H,当OD⊥BC、HA=HE时,求证:AB=CE;
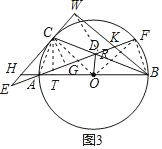
(3)如图3,在(2)的条件K在EF上,EH=![]() FK,S△ADO=
FK,S△ADO=![]() ,求WE的长.
,求WE的长.
【答案】(1)见解析;(2)见解析;(3)WE=![]()
【解析】
(1)应用切线性质和圆周角定理即可证得结论;
(2)过点C作CG⊥EF于G,连接BF,先证明△BDF≌△CDG(AAS),再证明△ABF≌△ECG(AAS),即可得出结论;
(3)先证明△ABD≌△ECA(ASA),再证明△ACD和△DEF为等腰直角三角形,设FK=a,BF=b,则DF=b,BD=CD=AC=![]() b,AD=
b,AD=![]() AC=2b,BC=2
AC=2b,BC=2![]() b,由勾股定理可得:OB=
b,由勾股定理可得:OB=![]() b,AB=CE=
b,AB=CE=![]() b,再根据S△ADO=
b,再根据S△ADO=![]() ,建立方程可求得b=1,过点C作CT⊥AB于T,过W作WR⊥EF于R,利用勾股定理和相似三角形性质即可求得WE.
,建立方程可求得b=1,过点C作CT⊥AB于T,过W作WR⊥EF于R,利用勾股定理和相似三角形性质即可求得WE.
(1)证明:如图1,连接OC,∵OB=OC
∴∠OCB=∠B
∵![]()
∴∠F=∠B
∴∠OCB=∠F
∵CE是⊙O切线,
∴OC⊥CE
∴∠OCE=90°
∵∠ECB=∠OCB+∠OCE
∴∠ECB=∠F+90°;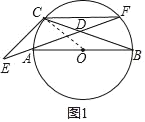
(2)证明:如图2,过点C作CG⊥EF于G,连接BF,则∠CGE=∠CGD=90°
∵AB是⊙O的直径,
∴∠AFB=90°=∠CGE=∠CGD
∵OD⊥BC
∴BD=CD
在△BDF和△CDG中,
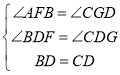 ,
,
∴△BDF≌△CDG(AAS)
∴BF=CG
∵HA=HE
∴∠EAH=∠E
∵∠BAF=∠EAH
∴∠BAF=∠E
在△ABF和△ECG中,
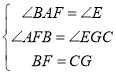 ,
,
∴△ABF≌△ECG(AAS)
∴AB=CE;
(3)如图3,过点C作CG⊥EF于G,连接AC,OC,OF,BF,
由(2)知:AB=CE,∠BAF=∠E
∵OA=OC
∴∠OCA=∠OAC
∵AB是⊙O的直径,CE是⊙O切线,
∴∠ACB=∠ECO=90°,即∠ECA+∠OCA=∠ABC+∠OAC
∴∠ECA=∠ABC
∴△ABD≌△ECA(ASA)
∴BD=AC
∵BD=CD
∴AC=CD
∴△ACD为等腰直角三角形
∴∠ADC=45°
∴∠EDF=45°
∴△DEF是等腰直角三角形
设FK=a,BF=b,则DF=b,BD=CD=AC=![]() b,AD=
b,AD=![]() AC=2b,BC=2
AC=2b,BC=2![]() b,
b,
∵BD=CD,OA=OB
∴OD=![]() AC=
AC=![]() b,
b,
∵∠BDO=90°
∴OB=![]() =
=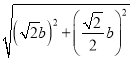 =
=![]() b
b
∴AB=CE=![]()
∵S△ADO=![]() ,
,
∴S△BOD=S△COD=![]() ,S△BOC=1
,S△BOC=1
∴![]() BCOD=1,即
BCOD=1,即![]() ×2
×2![]() b×
b×![]() b=1
b=1
∴b=1
∴AB=CE=![]() ,BF=1,AC=
,BF=1,AC=![]() ,BC=2
,BC=2![]()
∴AF=![]() =
=![]() =3
=3
过点C作CT⊥AB于T,则CT=![]() =
=![]() =
=![]() ,
,
∴OT=![]() =
=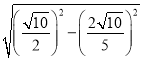 =
=![]() ,
,
∵tan∠COH=![]() ,
,
∴CHOT=CTOC,即:![]() CH=
CH=![]() ×
×![]()
∴CH=![]() ,
,
∵EH=![]() FK=
FK=![]() a,
a,
∴CH=CE﹣EH=![]() ﹣
﹣![]() a,
a,
∴![]() ﹣
﹣![]() a=
a=![]() ,解得:a=
,解得:a=![]() ,
,
∴FK=![]() ,EH=
,EH=![]() ,
,
∵△AEH∽△AFO
∴![]() =
=![]() ,即AEOA=AFEH,AE×
,即AEOA=AFEH,AE×![]() =3×
=3×![]() ,
,
∴AE=2,EK=AE+AF﹣FK=2+3﹣![]() =
=![]()
过W作WR⊥EF于R,易证:△BFK∽△WRK
∴![]() =
=![]() =
=![]() =
=![]() ,设KR=m,WR=2m
,设KR=m,WR=2m
∵![]() =tan∠WER=tan∠BAF=
=tan∠WER=tan∠BAF=![]() =
=![]()
∴![]() =
=![]() ,即ER=6m,
,即ER=6m,
∴EK=7m=![]() ,解得:m=
,解得:m=![]()
∴ER=6×![]() =
=![]() ,WR=2×
,WR=2×![]() =
=![]()
∴WE=![]() =
= =
=![]()


科目:初中数学 来源: 题型:
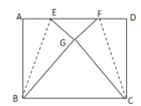
【题目】如图,在矩形ABCD中,2AB>BC,点E和点F为边AD上两点,将矩形沿着BE和CF折叠,点A和点D恰好重合于矩形内部的点G处,
(1)当AB=BC时,求∠GEF的度数;
(2)若AB=![]() ,BC=2,求EF的长.
,BC=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线l与坐标轴相交于A(2![]() ,0),B(0,
,0),B(0,![]() )两点,将Rt△AOB绕原点O逆时针旋转到Rt△A′OB′.
)两点,将Rt△AOB绕原点O逆时针旋转到Rt△A′OB′.
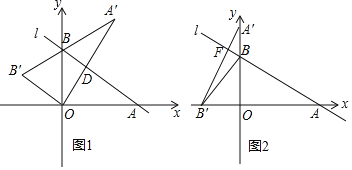
(1)求直线l的解析式;
(2)若OA′⊥AB,垂足为D,求点D的坐标;
(3)如图2,若将Rt△AOB绕原点O逆时针旋转90°,A′B′与直线l相交于点F,点E为x轴上一动点,试探究:是否存在点E,使得以点A,E,F为顶点的三角形和△A′BB′相似,若存在,请求出点E的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
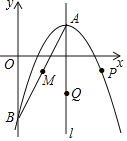
(1)求抛物线的表达式;
(2)写出点![]() 的坐标并求直线
的坐标并求直线![]() 的表达式;
的表达式;
(3)设动点![]() ,
,![]() 分别在抛物线和对称轴l上,当以
分别在抛物线和对称轴l上,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() ,
,![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
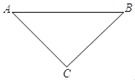
【题目】如图,在Rt△ABC中,AC=BC,AB=10,以AB为斜边向上作Rt△ABD,使∠ADB=90°.连接CD,若CD=7![]() ,则AD=_____.
,则AD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+3的图象过点A(﹣1,0),顶点坐标为(1,m).
(1)求该二次函数的关系式和m值;
(2)结合图象,解答下列问题:(直接写出答案)
①当x取什么值时,该函数的图象在x轴下方?
②当﹣1<x<2时,直接写出函数y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
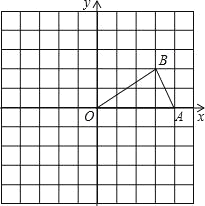
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
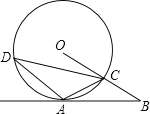
【题目】已知:如图A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,∠B=30°.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com