
【题目】如图,∠A=∠B=30°,P为AB中点,线段MV绕点P旋转,且M为射线AC上(不与点d重合)的任意一点,且N为射线BD上(不与点B重合)的一点,设∠BPN=α.
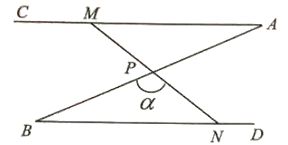
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若AB=4,60°≤α≤90°,直接写出△BPN的外心运动路线的长度。
【答案】(1)见解析;(2)30°;(3)![]()
【解析】
(1)由P为AB的中点,可得PA=PB,再由已知中∠A=∠B=30°,对顶角∠APM=∠BPN,根据ASA即可判定△APM≌△BPN;
(2)由(1)中结论可知PM=PN,即MN=2PN,由已知MN=2BN,可得BN=PN,根据等边对等角,即α=∠B=30°;
(3)当α=60°时,由∠B=30°,可知MN⊥BD,此时BP的中点为△BPN的外心,当α=90°时,由∠B=30°,此时BN的中点为△BPN的外心,根据三角形中位线定理可得△BPN的外心运动路线的长度为PN的一半,即为![]() .
.
(1)证明:∵P是AB的中点,∴PA=PB , 在△APM和△BPN中, 
∴△APM≌△BPN(ASA)
(2)解:由(1)得:△APM≌△BPN , ∴PM=PN , ∴MN=2PN , ∵MN=2BN , ∴BN=PN , ∴α=∠B=30°
(3)解: ![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
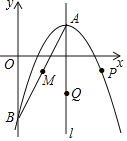
(1)求抛物线的表达式;
(2)写出点![]() 的坐标并求直线
的坐标并求直线![]() 的表达式;
的表达式;
(3)设动点![]() ,
,![]() 分别在抛物线和对称轴l上,当以
分别在抛物线和对称轴l上,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() ,
,![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接AE、DE.
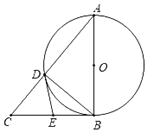
(1)求证:DE是⊙O的切线;
(2)设△CDE的面积为 S1,四边形ABED的面积为 S2.若 S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,若AE=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
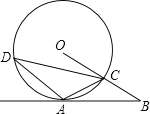
【题目】已知:如图A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,∠B=30°.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线x=2,且抛物线经过A(1,0),C(0,5)两点,与x轴交于点B.
的对称轴为直线x=2,且抛物线经过A(1,0),C(0,5)两点,与x轴交于点B.
(1)若直线y=mx+n经过B. C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作Q,使得Q与直线BC相切,在运动的过程中是否存在一个最大Q?若存在,请直接写出最大Q的半径;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:在直角△ABC中,如果较长的直角边的长度为较短直角边长度的两倍,则称直角△ABC为黄金三角形
(1)已知:点O(0,0),点A(2,0),下列y轴正半轴上的点能与点O,点A构成黄金三角形的有 ;填序号①(0,1);②(0,2);③(0,3),④(0,4);
(2)已知点P(5,0),判断直线y=2x-6在第一象限是否存在点Q,使得△OPQ是黄金三角形,若存在求出点Q的坐标,若不存在,说明理由;
(3)已知:反比例函数![]() 与直线y=-x+m+1交于M,N两点,若在x轴上有且只有一个点C,使得∠MCN=90
与直线y=-x+m+1交于M,N两点,若在x轴上有且只有一个点C,使得∠MCN=90![]() ,求m的值,并判断此时△MNC是否为黄金三角形.
,求m的值,并判断此时△MNC是否为黄金三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com