
ЎѕМвДїЎїОТГЗІ»·БФј¶ЁЈєФЪЦ±ЅЗЎчABCЦРЈ¬Из№ыЅПі¤µДЦ±ЅЗ±ЯµДі¤¶ИОЄЅП¶МЦ±ЅЗ±Яі¤¶ИµДБЅ±¶Ј¬ФтіЖЦ±ЅЗЎчABCОЄ»ЖЅрИэЅЗРО
ЈЁ1Ј©ТСЦЄЈєµгOЈЁ0Ј¬0Ј©Ј¬µгAЈЁ2Ј¬0Ј©Ј¬ПВБРyЦбХэ°лЦбЙПµДµгДЬУлµгOЈ¬µгA№№іЙ»ЖЅрИэЅЗРОµДУРЎЎЎЎЈ»МоРтєЕўЩЈЁ0Ј¬1Ј©Ј»ўЪЈЁ0Ј¬2Ј©Ј»ўЫЈЁ0Ј¬3Ј©Ј¬ўЬЈЁ0Ј¬4Ј©Ј»
ЈЁ2Ј©ТСЦЄµгPЈЁ5Ј¬0Ј©Ј¬ЕР¶ПЦ±ПЯy=2x-6ФЪµЪТ»ПуПЮКЗ·сґжФЪµгQЈ¬К№µГЎчOPQКЗ»ЖЅрИэЅЗРОЈ¬ИфґжФЪЗуіцµгQµДЧш±кЈ¬ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ»
ЈЁ3Ј©ТСЦЄЈє·ґ±ИАэєЇКэ![]() УлЦ±ПЯy=-x+m+1Ѕ»УЪMЈ¬NБЅµгЈ¬ИфФЪxЦбЙПУРЗТЦ»УРТ»ёцµгCЈ¬К№µГЎПMCN=90
УлЦ±ПЯy=-x+m+1Ѕ»УЪMЈ¬NБЅµгЈ¬ИфФЪxЦбЙПУРЗТЦ»УРТ»ёцµгCЈ¬К№µГЎПMCN=90![]() Ј¬ЗуmµДЦµЈ¬ІўЕР¶ПґЛК±ЎчMNCКЗ·сОЄ»ЖЅрИэЅЗРОЈ®
Ј¬ЗуmµДЦµЈ¬ІўЕР¶ПґЛК±ЎчMNCКЗ·сОЄ»ЖЅрИэЅЗРОЈ®
Ўѕґр°ёЎїЈЁ1Ј©ўЩўЬЈ»ЈЁ2Ј©QЧш±кОЄЈЁ5Ј¬4Ј©Ј»ЈЁ3Ј©КЗ»ЖЅрИэЅЗРО
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭ»ЖЅрИэЅЗРОµД¶ЁТејґїЙЕР¶ПЈ®
ЈЁ2Ј©јЩЙиґжФЪЈ®ЙиQ(m,2m6)Ј¬·ЦБЅЦЦЗйРО·Ц±рЗуЅвјґїЙЈ®
ЈЁ3Ј©ЙиM(x1,y1)Ј¬N(x2,y2)Ј¬MNµДЦРµгОЄkЈ¬µ±µгKµЅxЦбµДѕаАлµИУЪ![]() К±Ј¬ВъЧгМхјюЈ®ёщѕЭТ»ФЄ¶юґО·ЅіМµДёщУлПµКэµД№ШПµЈ¬№№ЅЁ·ЅіМЗуіцmјґїЙЕР¶ПЈ®
К±Ј¬ВъЧгМхјюЈ®ёщѕЭТ»ФЄ¶юґО·ЅіМµДёщУлПµКэµД№ШПµЈ¬№№ЅЁ·ЅіМЗуіцmјґїЙЕР¶ПЈ®
ЅвЈєЈЁ1Ј©ТтОЄµг![]() ЈЁ0Ј¬0Ј©Ј¬µг
ЈЁ0Ј¬0Ј©Ј¬µг![]() ЈЁ2Ј¬0Ј©Ј¬ёщѕЭ»ЖЅрИэЅЗРОµД¶ЁТеїЙЦЄФЪyЦбХэ°лЦбЙПµДµг
ЈЁ2Ј¬0Ј©Ј¬ёщѕЭ»ЖЅрИэЅЗРОµД¶ЁТеїЙЦЄФЪyЦбХэ°лЦбЙПµДµг
УлФµгµДПЯ¶Оі¤¶ИОЄ1»тХЯ4Ј¬№КЅбєПМвДїїЙЦЄУлµг![]() Ј¬µг
Ј¬µг![]() №№іЙ»ЖЅрИэЅЗРОµДУР
№№іЙ»ЖЅрИэЅЗРОµДУР![]() »т
»т![]() Ј¬№Кґр°ёОЄўЩўЬЈ®
Ј¬№Кґр°ёОЄўЩўЬЈ®
ЈЁ2Ј©јЩЙиґжФЪЈ®Йи![]() Ј¬
Ј¬
![]() КЗЦ±ЅЗИэЅЗРОЈ¬µ±
КЗЦ±ЅЗИэЅЗРОЈ¬µ±![]() КЗЦ±ЅЗИэЅЗРОК±Ј¬
КЗЦ±ЅЗИэЅЗРОК±Ј¬![]() Ј¬
Ј¬
![]() Ј¬ЅвµГЈє
Ј¬ЅвµГЈє![]() єН4Ј¬
єН4Ј¬
![]() µг
µг![]() ФЪµЪТ»ПуПЮЈ¬
ФЪµЪТ»ПуПЮЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() КЗ»ЖЅрИэЅЗРОЈ¬
КЗ»ЖЅрИэЅЗРОЈ¬
µ±![]() К±Ј¬
К±Ј¬![]() Ј¬ґЛК±
Ј¬ґЛК±![]() І»ВъЧг»ЖЅрИэЅЗРОµД¶ЁТеЈ®
І»ВъЧг»ЖЅрИэЅЗРОµД¶ЁТеЈ®
![]() ВъЧгМхјюµгµг
ВъЧгМхјюµгµг![]() Чш±кОЄ
Чш±кОЄ![]() Ј®
Ј®
ЈЁ3Ј©Йи![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() µДЦРµгОЄ
µДЦРµгОЄ![]() Ј¬µ±µг
Ј¬µ±µг![]() µЅ
µЅ![]() ЦбµДѕаАлµИУЪ
ЦбµДѕаАлµИУЪ![]() К±Ј¬ВъЧгМхјюЈ®
К±Ј¬ВъЧгМхјюЈ®
УЙ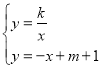 Ј¬ПыИҐ
Ј¬ПыИҐ![]() µГµЅЈє
µГµЅЈє![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј®
Ј®![]() Ј¬
Ј¬
![]()
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
![]() Ј¬
Ј¬
ХыАнµГЈє![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ИзНјЈ¬Чч![]() ЦбУЪ
ЦбУЪ![]() Ј®
Ј®
![]() Ц±ПЯ
Ц±ПЯ![]() µДЅвОцКЅОЄ
µДЅвОцКЅОЄ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() І»КЗ»ЖЅрИэЅЗРОЈ®
І»КЗ»ЖЅрИэЅЗРОЈ®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
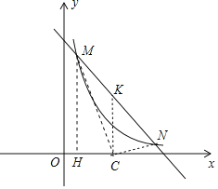
ЎѕМвДїЎїИзНјЈ¬ЎПA=ЎПB=30ЎгЈ¬PОЄABЦРµгЈ¬ПЯ¶ОMVИЖµгPРэЧЄЈ¬ЗТMОЄЙдПЯACЙПЈЁІ»УлµгdЦШєПЈ©µДИОТвТ»µгЈ¬ЗТNОЄЙдПЯBDЙПЈЁІ»УлµгBЦШєПЈ©µДТ»µгЈ¬ЙиЎПBPN=¦БЈ®
ЈЁ1Ј©ЗуЦ¤ЈєЎчAPMЎХЎчBPNЈ»
ЈЁ2Ј©µ±MN=2BNК±Ј¬Зу¦БµД¶ИКэЈ»
ЈЁ3Ј©ИфAB=4Ј¬60ЎгЎЬ¦БЎЬ90ЎгЈ¬Ц±ЅУРґіцЎчBPNµДНвРДФЛ¶ЇВ·ПЯµДі¤¶ИЎЈ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОКМв±іѕ°ЈєИзНј1Ј¬µИСьЎчABCЦРЈ¬AB=ACЈ¬ЎПBAC=120ЎгЈ¬ЧчADЎНBCУЪµгDЈ¬ФтDОЄBCµДЦРµгЈ¬ЎПBAD=![]() ЎПBAC=60ЎгЈ¬УЪКЗ
ЎПBAC=60ЎгЈ¬УЪКЗ![]() =
= ![]() =
=![]() Ј»
Ј»
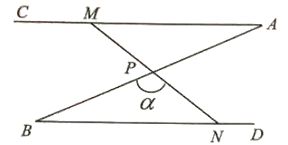
ЗЁТЖУ¦УГЈєИзНј2Ј¬ЎчABCєНЎчADE¶јКЗµИСьИэЅЗРОЈ¬ЎПBAC=ЎПDAE=120ЎгЈ¬DЈ¬EЈ¬CИэµгФЪН¬Т»МхЦ±ПЯЙПЈ¬Б¬ЅУBDЈ®
ўЩЗуЦ¤ЈєЎчADBЎХЎчAECЈ»
ўЪЗлЦ±ЅУРґіцПЯ¶ОADЈ¬BDЈ¬CDЦ®јдµДµИБї№ШПµКЅЈ»
НШХ№СУЙмЈєИзНј3Ј¬ФЪБвРОABCDЦРЈ¬ЎПABC=120ЎгЈ¬ФЪЎПABCДЪЧчЙдПЯBMЈ¬ЧчµгC№ШУЪBMµД¶ФіЖµгEЈ¬Б¬ЅУAEІўСУі¤Ѕ»BMУЪµгFЈ¬Б¬ЅУCEЈ¬CFЈ®
ўЩЦ¤ГчЎчCEFКЗµИ±ЯИэЅЗРОЈ»
ўЪИфAE=5Ј¬CE=2Ј¬ЗуBFµДі¤Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ѕШРОABCGЈЁABЈјBCЈ©УлѕШРОCDEFИ«µИЈ¬µгBЈ¬CЈ¬DФЪН¬Т»МхЦ±ПЯЙПЈ¬ЎПAPEµД¶ҐµгPФЪПЯ¶ОBDЙПТЖ¶ЇЈ¬К№ЎПAPEОЄЦ±ЅЗµДµгPµДёцКэКЗЈЁ Ј©

AЈ®0 BЈ®1 CЈ®2 DЈ®3
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪµИСьЦ±ЅЗЎчABCЦРЈ¬ЎПC=90ЎгЈ¬DОЄBCµДЦРµгЈ¬Ѕ«ЎчABCХЫµюЈ¬К№µгAУлµгDЦШєПЈ¬EFОЄХЫєЫЈ¬ФтsinЎПBEDµДЦµКЗЈЁЎЎЎЎЈ©

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЎчABC µДГж»эОЄ 63Ј¬D КЗ BC ЙПµДТ»µгЈ¬ЗТ BDЈєBCЈЅ2Јє3Ј¬ DEЎОAC Ѕ» AB УЪµг EЈ¬СУі¤ DE µЅ FЈ¬К№ FEЈєEDЈЅ2Јє1Ј®Б¬Ѕб CF Ѕ» AB µгУЪ GЈ®
(1)ЗуЎчBDE µДГж»эЈ»
(2)Зу ![]() µДЦµЈ»
µДЦµЈ»
(3)ЗуЎчACG µДГж»эЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЈєИзНјЈ¬ФЪЎчABCЦРЈ¬ABЈЅ13Ј¬ACЈЅ8Ј¬cosЎПBACЈЅ![]() Ј¬BDЎНACЈ¬ґ№ЧгОЄµгDЈ¬EКЗBDµДЦРµгЈ¬БЄЅбAEІўСУі¤Ј¬Ѕ»±ЯBCУЪµгFЈ®
Ј¬BDЎНACЈ¬ґ№ЧгОЄµгDЈ¬EКЗBDµДЦРµгЈ¬БЄЅбAEІўСУі¤Ј¬Ѕ»±ЯBCУЪµгFЈ®
ЈЁ1Ј©ЗуЎПEADµДУаЗРЦµЈ»
ЈЁ2Ј©Зу![]() µДЦµЈ®
µДЦµЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
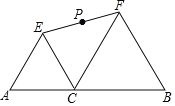
ЎѕМвДїЎїИзНјЈ¬ПЯ¶ОAB=2Ј¬CКЗABЙПТ»¶ЇµгЈ¬ТФACЎўBCОЄ±ЯФЪABН¬ІаЧчХэЎчACEЎўХэЎчBCFЈ¬Б¬EFЈ¬µгPОЄEFµДЦРµгЈ®µ±µгCґУAФЛ¶ЇµЅBК±Ј¬PµгФЛ¶ЇВ·ѕ¶і¤ОЄ____Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЈєИзНј1Ј¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬Ц±ПЯ1ЈєyЈЅ©Ѓx+4УлЧш±кЦб·Ц±рПаЅ»УЪµгAЎўBУлl2ЈєyЈЅ![]() xПаЅ»УЪµгCЈ®
xПаЅ»УЪµгCЈ®

ЈЁ1Ј©ЗуµгCµДЧш±кЈ»
ЈЁ2Ј©ИфЖЅРРУЪyЦбµДЦ±ПЯxЈЅaЅ»УЪЦ±ПЯ1УЪµгEЈ¬Ѕ»Ц±ПЯl2УЪµгDЈ¬Ѕ»xЦбУЪµгMЈ¬ЗТEDЈЅ2DMЈ¬ЗуaµДЦµЈ»
ЈЁ3Ј©ИзНј2Ј¬µгPКЗµЪЛДПуПЮДЪТ»µгЈ¬ЗТЎПBPOЈЅ135ЎгЈ¬Б¬ЅУAPЈ¬МЅѕїAPУлBPЦ®јдµДО»ЦГ№ШПµЈ¬ІўЦ¤ГчДгµДЅбВЫЈ®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com