
【题目】已知:如图1,在平面直角坐标系中,直线1:y=﹣x+4与坐标轴分别相交于点A、B与l2:y=![]() x相交于点C.
x相交于点C.

(1)求点C的坐标;
(2)若平行于y轴的直线x=a交于直线1于点E,交直线l2于点D,交x轴于点M,且ED=2DM,求a的值;
(3)如图2,点P是第四象限内一点,且∠BPO=135°,连接AP,探究AP与BP之间的位置关系,并证明你的结论.
【答案】(1)(3,1);(2)a=2或6;(3)AP⊥BP,证明见解析.
【解析】
(1)联立两直线解析式得到方程组,求出方程组的解即可确定出C的坐标;
(2)将x=1代入两直线方程求出对应y的值,确定出D与E的纵坐标,即OD与OE的长,由OE﹣OD求出DE的长,根据ED=2DM,求出MN的长,将x=a代入两直线方程,求出M与N对应的横坐标,相减的绝对值等于MN的长列出关于a的方程,求出方程的解即可求出a的值;
(3)AP⊥BP,理由为:过O作OQ⊥OP,交BP的延长线于点Q,由∠BPO为135°,得到∠OPQ为45°,又∠POQ为直角,可得出三角形OPQ为等腰直角三角形,再利用两对对应边成比例且夹角相等的两三角形相似得到三角形AOP与三角形BOQ相似,由相似三角形的对应角相等得到∠APO=∠BQO=45°,由∠BPO﹣∠APO得到∠APB为直角,即AP⊥BP.
(1)联立两直线解析式得: ,解得:
,解得:![]() ,则C坐标为(3,1);
,则C坐标为(3,1);
(2)由题意:M(a,0)D(a,![]() a) E(a,﹣a+4).
a) E(a,﹣a+4).
∵DE=2DM,∴|![]() a﹣(﹣a+4)|=2|
a﹣(﹣a+4)|=2|![]() a|,解得:a=2或6.
a|,解得:a=2或6.
(3)如图2中,过O作OQ⊥OP,交BP的延长线于点Q,可得∠POQ=90°.
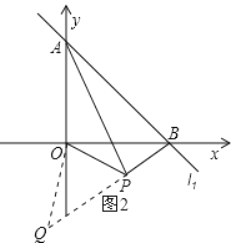
∵∠BPO=135°,∴∠OPQ=45°,∴∠Q=∠OPQ=45°,∴△POQ为等腰直角三角形,∴OP=OQ.
∵∠AOB=∠POQ=90°,∴∠AOB+∠BOP=∠POQ+∠POB,即∠AOP=∠BOQ.
∵OA=OB=4,∴![]() ,∴△AOP∽△BOQ,∴∠APO=∠BQO=45°,∴∠APB=∠BPO﹣∠APO=90°,则AP⊥BP.
,∴△AOP∽△BOQ,∴∠APO=∠BQO=45°,∴∠APB=∠BPO﹣∠APO=90°,则AP⊥BP.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】我们不妨约定:在直角△ABC中,如果较长的直角边的长度为较短直角边长度的两倍,则称直角△ABC为黄金三角形
(1)已知:点O(0,0),点A(2,0),下列y轴正半轴上的点能与点O,点A构成黄金三角形的有 ;填序号①(0,1);②(0,2);③(0,3),④(0,4);
(2)已知点P(5,0),判断直线y=2x-6在第一象限是否存在点Q,使得△OPQ是黄金三角形,若存在求出点Q的坐标,若不存在,说明理由;
(3)已知:反比例函数![]() 与直线y=-x+m+1交于M,N两点,若在x轴上有且只有一个点C,使得∠MCN=90
与直线y=-x+m+1交于M,N两点,若在x轴上有且只有一个点C,使得∠MCN=90![]() ,求m的值,并判断此时△MNC是否为黄金三角形.
,求m的值,并判断此时△MNC是否为黄金三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
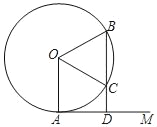
【题目】已知:如图,AM为⊙O的切线,A为切点.过⊙O上一点B作BD⊥AM于点D,BD交⊙O于点C,OC平分∠AOB.
(1)求∠AOB的度数;
(2)当⊙O的半径为4cm时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
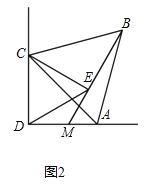
【题目】△ABC和△ECD都是等边三角形,△EBC可以看作是△DAC经过平移、轴对称或旋转得到.
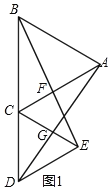
(1)如图1,当B,C,D在同一直线上,AC交BE于点F,AD交CE于点G,求证:CF=CG;
(2)如图2,当△ABC绕点C旋转至AD⊥CD时,连接BE并延长交AD于M,求证:MD=ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有_____.
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有_____.
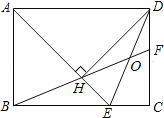
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+m与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)不解关于x、y的方程组直接写出点B的坐标;
(3)直线y=﹣2x+4m经过点B吗?请说明理由.
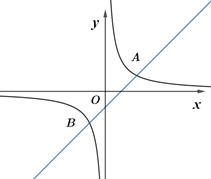
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
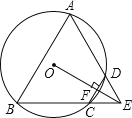
(1)求证:∠A=∠AEB.
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com