
【题目】已知关于x的一元二次方程ax2+bx=0 (a≠0)的一个根是x=2018,,则方程a(x+2)2+bx+2b=0的根是___________________.
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
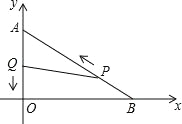
【题目】如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发运动时间为t(s).
(1)t为何值时,△APQ与△AOB相似?
(2)当 t为何值时,△APQ的面积为8cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县古田镇某纪念品商店在销售中发现:“成功从这里开始”的纪念品平均每天可售出20件,每件盈利40元.为了扩大销售量,增加盈利,尽快减少库存,该商店在今年国庆黄金周期间,采取了适当的降价措施,改变营销策略后发现:如果每件降价4元,那么平均每天就可多售出8件.商店要想平均每天在销售这种纪念品上盈利1200元,那么每件纪念品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
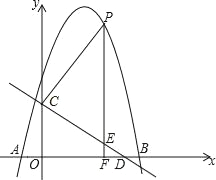
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)求PE的长最大时m的值.
(3)Q是平面直角坐标系内一点,在(2)的情况下,以PQCD为顶点的四边形是平行四边形是否存在?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
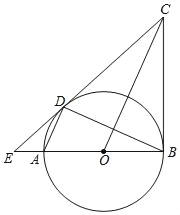
【题目】如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
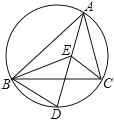
【题目】如图,点 E 是△ABC 的内心,AE 的延长线和△ABC 的外接圆相交于点 D,连 接 BE
(1) 若∠CBD=35°,求∠BAC 及∠BEC 的度数
(2) 求证:DE=DB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的图象如图,则下列结论:①abc>0;②a+b+c=2;③b2﹣4ac<0;④b<2a.其中正确的结论是( )
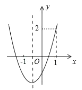
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:

请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小颖同学共调查了多少名居民的年龄,扇形统计图中a,b各等于多少?
(2)补全条形统计图;
(3)若该辖区年龄在0~14岁的居民约有1500人,请估计年龄在15~59岁的居民的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com