
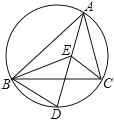
【题目】如图,点 E 是△ABC 的内心,AE 的延长线和△ABC 的外接圆相交于点 D,连 接 BE
(1) 若∠CBD=35°,求∠BAC 及∠BEC 的度数
(2) 求证:DE=DB
【答案】(1) 125°;(2)见详解.
【解析】
(1)根据三角形的内心是三条角平分线的交点,得到∠BAC=2∠CAD,∠ABC=2∠EBC,∠ACB=∠ECB,再用三角形内角和求出∠BEC;
(2)由三角形的内心E得到∠BAD=∠CAD,∠EBA=∠EBC,经过等量代换得∠DEB=∠DBE,所以DE=DB.
(1)在外接圆中,∵∠CBD=35°,
∵∠CAD=35°,
∵点E是△ABC的内心,
∴∠BAC=2∠CAD =70°,
∴∠EBC+∠ECB=(180°-70°)÷2=55°,
∴∠BEC=180°-55°=125°.
(2) 证明:∵E是△ABC的内心,
∴∠BAD=∠CAD,∠EBA=∠EBC,
∵∠DEB=∠BAD +∠EBA,∠DBE=∠EBC +∠CBD,∠CBD =∠CAD,
∴∠DEB=∠DBE,
∴DE=DB.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
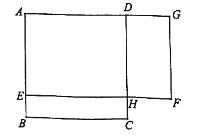
【题目】如图, ![]() 是一块边长为4米的正方形苗圃,园林部门将其改造为矩形
是一块边长为4米的正方形苗圃,园林部门将其改造为矩形![]() 的形状,其中点
的形状,其中点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 的延长线上,
的延长线上, ![]() 设
设![]() 的长为
的长为![]() 米,改造后苗圃
米,改造后苗圃![]() 的面积为
的面积为![]() 平方米.
平方米.
(1) ![]() 与
与![]() 之间的函数关系式为 (不需写自变量的取值范围);
之间的函数关系式为 (不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃![]() 的面积与原正方形苗圃
的面积与原正方形苗圃![]() 的面积相等,请问此时
的面积相等,请问此时![]() 的长为多少米?
的长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
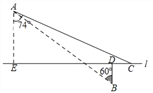
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx=0 (a≠0)的一个根是x=2018,,则方程a(x+2)2+bx+2b=0的根是___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() O
O![]() 中的点P和⊙C,给出如下定义:若⊙C上存在两个点M,N,使得∠MPN=60°,则称P为⊙C 的关联点。已知点D(
中的点P和⊙C,给出如下定义:若⊙C上存在两个点M,N,使得∠MPN=60°,则称P为⊙C 的关联点。已知点D(![]() ,
,![]() ),E(0,-2),F(
),E(0,-2),F(![]() ,0)
,0)
(1)当⊙O的半径为1时,
①在点O,D,E,F中,⊙O的关联点是______ ____;
②如果G(0,t)是⊙O的关联点,则t的取值范围是 ;
(2)如果线段EF上每一个点都是⊙O的关联点,那么⊙O的半径![]() 最小为 ;
最小为 ;
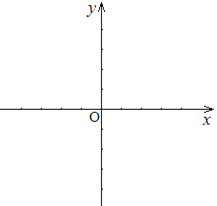
(3)Rt⊿ABC中,∠C=90![]() ,BC=8,∠A=30
,BC=8,∠A=30![]() ,⊙P的半径为1,当点P运动时,始终确保⊿ABC的三条边中至少有一条边上恰好有唯一的⊙P的关联点。请你画出点P所走过的路线围成的图形的示意图,并在下面横线上直接写出它的总长。
,⊙P的半径为1,当点P运动时,始终确保⊿ABC的三条边中至少有一条边上恰好有唯一的⊙P的关联点。请你画出点P所走过的路线围成的图形的示意图,并在下面横线上直接写出它的总长。

答:点P经过的路线围成的图形的总长为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为60元/件的T恤,规定试销期间单价不低于成本单价,又获利不得高于40%,经试销发现,销售量y(件)与销售单价x(元/件)符合一次函数y=kx+b,且x=70时,y=50;x=80时,y=40;
(1)求出一次函数y=kx+b的解析式
(2)若该商场获得利润为w元,试写出利润w与销售单价x之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
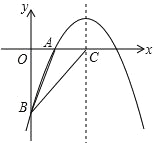
【题目】如图,二次函数 y=﹣x2+bx+c 的图象经过 A(1,0),B(0,﹣3)两点.
(1)求这个抛物线的解析式及顶点坐标;
(2)设该二次函数的对称轴与 x 轴交于点 C,连接 BA、BC,求△ABC 的面积.
(3)在抛物线的对称轴上是否存在一点 P,使得 O、B、C、P 四点为顶点的四边形是平行四边形?若存在,请直接写出 P 点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com