
����Ŀ��ij�̳�����һ�ֳɱ�Ϊ60Ԫ/����T�����涨�����ڼ䵥�۲����ڳɱ����ۣ��ֻ������ø���40%�����������֣�������y�����������۵���x��Ԫ/��������һ�κ���y��kx+b����x��70ʱ��y��50��x��80ʱ��y��40��
��1�����һ�κ���y��kx+b�Ľ���ʽ
��2�������̳��������ΪwԪ����д������w�����۵���x֮��Ĺ�ϵʽ�����۵��۶�Ϊ����ʱ���̳��ɻ�����������������Ƕ��٣�
���𰸡���1��y����x+120����2�������ۼ۶�Ϊ84Ԫ/��ʱ���̳����Ի������������������864Ԫ��
��������
��1�����ô���ϵ������ȷ��һ�κ����Ľ���ʽ��
��2����������������������������Ȼ��1���еĺ���ʽ�������У������������۵���֮��Ĺ�ϵʽ��Ȼ��������������жϳ��������
��1��������ã�![]() ��
��
��![]() ��
��
��һ�κ����Ľ���ʽΪ��y����x+120��
��2��w����x��60������x+120������x2+180x��7200������x��90��2+900��
�������߿������£�
�൱x��90ʱ��w��x�����������
��60��x��84��
�൱x��84ʱ��w����84��60������120��84����864��
�𣺵����ۼ۶�Ϊ84Ԫ/��ʱ���̳����Ի������������������864Ԫ��


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
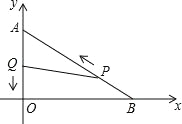
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪OA��6���ף�OB��8���ף���P�ӵ�B��ʼ��BA�����յ�A��1����/����ٶ��ƶ�����Q�ӵ�A��ʼ��AO�����յ�O��1����/����ٶ��ƶ�.��P��Qͬʱ�����˶�ʱ��Ϊt(s).
��1��tΪ��ֵʱ����APQ����AOB���ƣ�
��2���� tΪ��ֵʱ����APQ�����Ϊ8cm2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
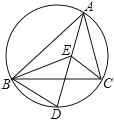
����Ŀ����ͼ���� E ����ABC ��������AE ���ӳ��ߺ���ABC �����Բ�ཻ�ڵ� D���� �� BE
(1) ����CBD��35�㣬���BAC ����BEC �Ķ���
(2) ��֤��DE��DB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��ͼ����ͼ�������н��ۣ���abc��0����a+b+c=2����b2��4ac��0����b��2a��������ȷ�Ľ����ǣ�������
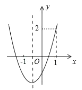
A. �٢� B. �ڢ� C. �ڢ� D. �ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���![]() �У�
��![]() ��
��![]() ����
����![]() �ǣ�
�ǣ�![]() ����ֱ�����ǰ�
����ֱ�����ǰ�![]() ����ͼ����ͼ��ƽ�ƣ�ֱ�DZ�
����ͼ����ͼ��ƽ�ƣ�ֱ�DZ�![]() ������
������![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ��ӳ�
�ϣ��ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() ����
����![]() ��
��![]() �����
�����![]() �ӵ�
�ӵ�![]() ƽ�Ƶ���
ƽ�Ƶ���![]() �Ĺ����У���
�Ĺ����У���![]() ���˶�·����Ϊ__________��
���˶�·����Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶ�������֪Բ���ڽ������������ij߹���ͼ����.
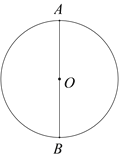
��֪����O��
��������O���ڽ��������Σ�
��������ͼ��
����ֱ��AB��
����BΪԲ�ģ�OBΪ�뾶���������O����C��D���㣻
������AC��AD��CD��
���ԡ�ACD��������������Σ�
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤�����ڡ�O�У�����OC��OD��BC��BD��
��OC=OB=BC��
���OBCΪ�ȱ������Σ�_______________���������������ݣ���
���BOC=60�㣮
���AOC=180��-��BOC=120�㣮
ͬ����AOD=120�㣬
���COD=��AOC=��AOD=120�㣮
��AC=CD=AD��_______________���������������ݣ���
���ACD�ǵȱ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��ԲO��ֱ������CD��AB������H�ڰ뾶OB�ϣ�AH=5��CD=![]() ����E�ڻ�AD�ϣ�����AE��CD���ӳ��߽��ڵ�F��
����E�ڻ�AD�ϣ�����AE��CD���ӳ��߽��ڵ�F��
��1����ԲO�İ뾶��
��2�����AE=6����EF�ij���
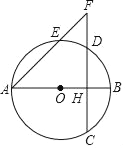
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сӱͬѧѧ��ͳ��֪ʶ�������������������Ͻ����������������������������ݻ��Ƴ��������κ�����ͳ��ͼ��

��������ϲ�������ͳ��ͼ�ṩ����Ϣ���������������
��1��Сӱͬѧ�������˶��������������������ͳ��ͼ��a��b�����ڶ��٣�
��2����ȫ����ͳ��ͼ��
��3������Ͻ��������0��14��ľ���Լ��1500���������������15��59��ľ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ����ABC�ڽ�����O��AB=AC��BDΪ��O���ң���AB��CD������A����O������AE��DC���ӳ��߽��ڵ�E��AD��BC���ڵ�F��

��1����֤���ı���ABCE��ƽ���ı��Σ�
��2����AE=6��CD=5����OF�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com