
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
【答案】(1)-2;(2)2.
【解析】
(1)利用判别式的意义得到△=(2m+1)2﹣4(m2﹣2)≥0,然后解不等式得到m的范围,再在此范围内找出最小整数值即可;
(2)利用根与系数的关系得到x1+x2=﹣(2m+1),x1x2=m2﹣2,再利用(x1﹣x2)2+m2=21得到(2m+1)2﹣4(m2﹣2)+m2=21,接着解关于m的方程,然后利用(1)中m的范围确定m的值.
(1)根据题意得△=(2m+1)2﹣4(m2﹣2)≥0,
解得m≥﹣![]() ,
,
所以m的最小整数值为﹣2;
(2)根据题意得x1+x2=﹣(2m+1),x1x2=m2﹣2,
∵(x1﹣x2)2+m2=21,
∴(x1+x2)2﹣4x1x2+m2=21,
∴(2m+1)2﹣4(m2﹣2)+m2=21,
整理得m2+4m﹣12=0,解得m1=2,m2=﹣6,
∵m≥﹣![]() ,
,
∴m的值为2.


科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
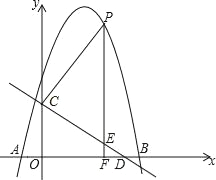
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)求PE的长最大时m的值.
(3)Q是平面直角坐标系内一点,在(2)的情况下,以PQCD为顶点的四边形是平行四边形是否存在?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
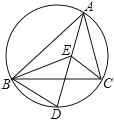
【题目】如图,点 E 是△ABC 的内心,AE 的延长线和△ABC 的外接圆相交于点 D,连 接 BE
(1) 若∠CBD=35°,求∠BAC 及∠BEC 的度数
(2) 求证:DE=DB
查看答案和解析>>
科目:初中数学 来源: 题型:
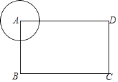
【题目】如图:矩形ABCD中AB=2,BC= ![]() ,⊙A是以A为圆心,半径r=1的圆,若⊙A绕着点B顺时针旋转,旋转角为α( 0°<α<180°);当旋转后的圆与矩形ABCD的边相切时,α=________度.
,⊙A是以A为圆心,半径r=1的圆,若⊙A绕着点B顺时针旋转,旋转角为α( 0°<α<180°);当旋转后的圆与矩形ABCD的边相切时,α=________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的图象如图,则下列结论:①abc>0;②a+b+c=2;③b2﹣4ac<0;④b<2a.其中正确的结论是( )
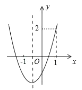
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 中,
中,![]() ,
,![]() ,含
,含![]() 角(
角(![]() )的直角三角板
)的直角三角板![]() (如图)在图中平移,直角边
(如图)在图中平移,直角边![]() ,顶点
,顶点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,延长
上,延长![]() 到点
到点![]() ,使
,使![]() ,若
,若![]() ,
,![]() ,则点
,则点![]() 从点
从点![]() 平移到点
平移到点![]() 的过程中,点
的过程中,点![]() 的运动路径长为__________.
的运动路径长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
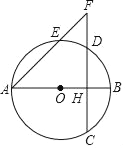
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足H在半径OB上,AH=5,CD=![]() ,点E在弧AD上,射线AE与CD的延长线交于点F.
,点E在弧AD上,射线AE与CD的延长线交于点F.
(1)求圆O的半径;
(2)如果AE=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求当10≤t≤30时,R和t之间的关系式;
(2)求温度在30℃时电阻R的值;并求出t≥30时,R和t之间的关系式;
(3)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过6 kΩ?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com