
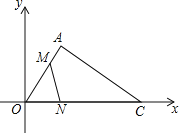
【题目】如图,点O是平面直角坐标系的原点,点A(![]() ,3),AC⊥OA与x轴的交点为C.动点M以每秒
,3),AC⊥OA与x轴的交点为C.动点M以每秒![]() 个单位长度由点A向点O运动.同时,动点N以每秒3个单位长度由点O向点C运动,当一动点先到终点时,另一动点立即停止运动.
个单位长度由点A向点O运动.同时,动点N以每秒3个单位长度由点O向点C运动,当一动点先到终点时,另一动点立即停止运动.
(1)写出∠AOC的值;
(2)用t表示出四边形AMNC的面积;
(3)求点P的坐标,使得以O、N、M、P为顶点的四边形是特殊的平行四边形?
【答案】(1)30°;(2)![]() ;(3)
;(3)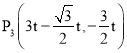 .
.
【解析】
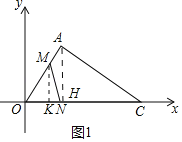
(1)如图1中,作AH⊥OC于H.在Rt△AOH中,解直角三角形求出∠AOH即可解决问题.
(2)作MK⊥BC于K.根据S四边形AMNC=S△OAC﹣S△OMN,计算即可.
(3)分别考虑以OM,ON,MN为平行四边形的对角线,利用平行四边形的性质求解即可.
解:(1)如图1中,作AH⊥OC于H.
∵A(![]() ,3),
,3),
∴OH=![]() ,AH=3,
,AH=3,
∴tan∠AOH=![]() =
=![]() ,
,
∴∠AOH=60°,
∵OA⊥AC,
∴∠OAC=90°,
∴∠ACO=30°.
(2)作MK⊥BC于K.
在Rt△AOH中,∵OH=![]() ,∠OAH=30°,
,∠OAH=30°,
∴OA=2OH=2![]() ,
,
在Rt△AOC中,∵∠AOC=30°,OA=2![]() ,
,
∴AC=![]() OA=6,
OA=6,
∵OM=![]() t,
t,
∴MK=OMsin60°=![]() t,
t,
∴S四边形AMNC=S△OAC﹣S△OMN
=![]() OAAC﹣
OAAC﹣![]() ONMKa
ONMKa
=![]() ×2
×2![]() ×6﹣
×6﹣![]() ×3t×
×3t×![]() t
t
=6![]() ﹣
﹣![]() t2(0<t<2).
t2(0<t<2).
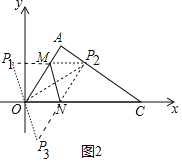
(3)当四边形CNMP1是平行四边形时,P1(![]() t﹣3t,
t﹣3t,![]() t).
t).
当四边形ONP2M是平行四边形时,P2(![]() t+3t,
t+3t,![]() t).
t).
当四边形OMNP3是平行四边形时,P3(3t﹣![]() t,﹣
t,﹣![]() t).
t).


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的⊙
为直径的⊙![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .
.
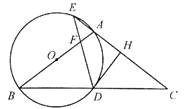
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若⊙![]() 的半径为4,①当
的半径为4,①当![]() 时,求
时,求![]() 的长(结果保留π);②当
的长(结果保留π);②当![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从沈阳到大连的火车原来的平均速度是180千米/时,经过两次提速后平均速度为217.8干米/时,这两次提速的百分率相同.
(1)求该火车每次提速的百分率;
(2)填空:若沈阳到大连的铁路长396千米,则第一次提速后从甲地到乙地所用的时间比提速前少用了 小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
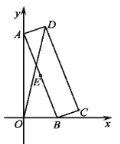
【题目】如图,矩形硬纸片ABCD的顶点A在![]() 轴的正半轴及原点上滑动,顶点B在
轴的正半轴及原点上滑动,顶点B在![]() 轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为
轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为![]() ,其中正确的结论是_________(填写序号).
,其中正确的结论是_________(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
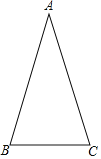
【题目】 如图,在△ABC中,AB=AC.
(1)用尺规作图法在AC边上找一点D,使得BD=BC(保留作图痕迹,不要求写作法):
(2)若∠A=30°,求∠ABD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
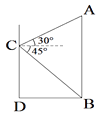
【题目】某数学兴趣小组的同学在一次活动中,为了测量某建筑物AB的高,他们来到另一建筑物CD上的点C处进行观察,如图所示,他们测得建筑物AB顶部A的仰角为30°,底部B的俯角为45°,已知建筑物AB、CD的距离DB为12m,求建筑物AB的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校每学期都要对优秀的学生进行表扬,而每班采取民主投票的方式进行选举,然后把名单报到学校.若每个班级平均分到3位三好生、4位模范生、5位成绩提高奖的名额,且各项均不能兼得、现在学校有30个班级,平均每班50人.
(1)作为一名学生,你恰好能得到荣誉的机会有多大?
(2)作为一名学生,你恰好能当选三好生、模范生的机会有多大?
(3)在全校学生数、班级人数、三好生数、模范生数、成绩提高奖人数中,哪些是解决上面两个问题所需要的?
(4)你可以用哪些方法来模拟实验?
查看答案和解析>>
科目:初中数学 来源: 题型:
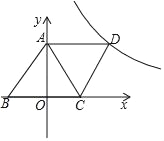
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A(0,4),B(﹣3,0)反比例函数y=![]() (k为常数,k≠0,x>0)的图象经过点D.
(k为常数,k≠0,x>0)的图象经过点D.
(1)填空:k=_____.
(2)已知在y=![]() 的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面在角坐标系中,抛物线y=x2-2x-3与x轴交与点A,B(点A在点B的左侧)交y轴于点C,点D为抛物线的顶点,对称轴与x轴交于点E.
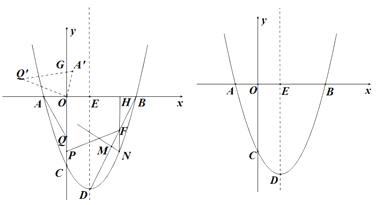
(1)连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当MN取得最大值时,求HF+FP+![]() PC的最小值;
PC的最小值;
(2)在(1)中,当MN取得最大值HF+FP+1/3PC取得小值时,把点P向上平移个![]() 单位得到点Q,连结AQ,把△AOQ绕点O瓶时针旋转一定的角度
单位得到点Q,连结AQ,把△AOQ绕点O瓶时针旋转一定的角度![]() (0°<
(0°<![]() <360°),得到△AOQ,其中边AQ交坐标轴于点C在旋转过程中,是否存在一点G使得
<360°),得到△AOQ,其中边AQ交坐标轴于点C在旋转过程中,是否存在一点G使得![]() ?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com