
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的⊙
为直径的⊙![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .
.
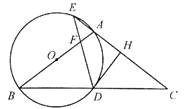
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若⊙![]() 的半径为4,①当
的半径为4,①当![]() 时,求
时,求![]() 的长(结果保留π);②当
的长(结果保留π);②当![]() 时,求线段
时,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)①![]() 的长=
的长=![]() ;②AF=
;②AF=![]() .
.
【解析】
(1)根据同圆的半径相等和等边对等角证明:∠ODB=∠OBD=∠ACB,则DH⊥OD,DH是圆O的切线;
(2)①根据等腰三角形的性质的∠EAF=∠EAF,设∠B=∠C=α,得到∠EAF=∠EFA=2α,根据三角形的内角和得到∠B=36°,求得∠AOD=72°,根据弧长公式即可得到结论;
②连接AD,根据圆周角定理得到∠ADB=∠ADC=90°,解直角三角形得到AD=![]() ,根据相似三角形的性质得到AH=3,于是得到结论.
,根据相似三角形的性质得到AH=3,于是得到结论.
(1)连接OD,如图,
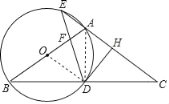
∵OB=OD,
∴△ODB是等腰三角形,
∠OBD=∠ODB①,
在△ABC中,∵AB=AC,
∴∠ABC=∠ACB②,
由①②得:∠ODB=∠OBD=∠ACB,
∴OD∥AC,
∵DH⊥AC,
∴DH⊥OD,
∴DH是圆O的切线;
(2)①∵AE=EF,
∴∠EAF=∠EAF,
设∠B=∠C=α,
∴∠EAF=∠EFA=2α,
∵∠E=∠B=α,
∴α+2α+2α=180°,
∴α=36°,
∴∠B=36°,
∴∠AOD=72°,
∴![]() 的长=
的长=![]() ;
;
②连接AD,
∵AB为⊙O的直径,
∴∠ADB=∠ADC=90°,
∵⊙O的半径为4,
∴AB=AC=8,
∵![]() ,
,
∴![]() ,
,
∴AD=2![]() ,
,
∵AD⊥BC,DH⊥AC,
∴△ADH∽△ACD,
∴![]() ,
,
∴![]() ,
,
∴AH=3,
∴CH=5,
∵∠B=∠C,∠E=∠B,
∴∠E=∠C,
∴DE=DC,∵DH⊥AC,
∴EH=CH=5,
∴AE=2,
∵OD∥AC,
∴∠EAF=∠FOD,∠E=∠FDO,
∴△AEF∽△ODF,
∴![]() ,
,
∴![]() ,
,
∴AF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
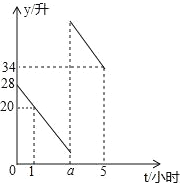
(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
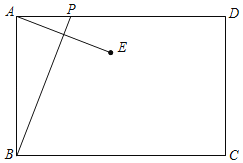
【题目】如图,已知矩形ABCD中,AB=4,动点P从点A出发,沿AD方向以每秒1个单位的速度运动,连接BP,作点A关于直线BP的对称点E,设点P的运动时间为t(s).
(1)若AD=6,P仅在边AD运动,求当P,E,C三点在同一直线上时对应的t的值.
(2)在动点P在射线AD上运动的过程中,求使点E到直线BC的距离等于3时对应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条长1200 m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
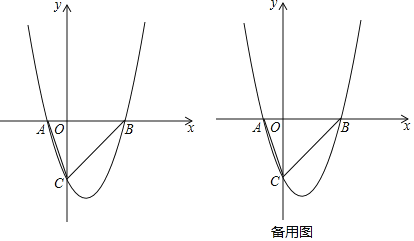
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(x1,0)、B(x2,0),与y轴交于点C(0,﹣x2),且x1<0<x2, ![]() ,△ABC的面积为6.
,△ABC的面积为6.
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上是否存在一点M,使四边形ABMC的面积最大?若存在,请求出点M的坐标和四边形ABMC的面积最大值;若不存在,请说明理由;
(3)E为抛物线的对称轴上一点,抛物线上是否存在一点D,使以B、C、D、E为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
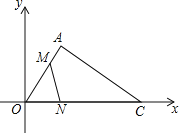
【题目】如图,点O是平面直角坐标系的原点,点A(![]() ,3),AC⊥OA与x轴的交点为C.动点M以每秒
,3),AC⊥OA与x轴的交点为C.动点M以每秒![]() 个单位长度由点A向点O运动.同时,动点N以每秒3个单位长度由点O向点C运动,当一动点先到终点时,另一动点立即停止运动.
个单位长度由点A向点O运动.同时,动点N以每秒3个单位长度由点O向点C运动,当一动点先到终点时,另一动点立即停止运动.
(1)写出∠AOC的值;
(2)用t表示出四边形AMNC的面积;
(3)求点P的坐标,使得以O、N、M、P为顶点的四边形是特殊的平行四边形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com