
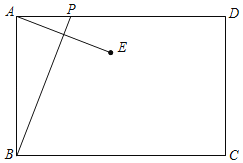
【题目】如图,已知矩形ABCD中,AB=4,动点P从点A出发,沿AD方向以每秒1个单位的速度运动,连接BP,作点A关于直线BP的对称点E,设点P的运动时间为t(s).
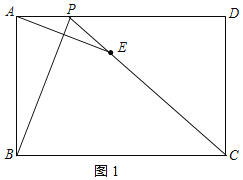
(1)若AD=6,P仅在边AD运动,求当P,E,C三点在同一直线上时对应的t的值.
(2)在动点P在射线AD上运动的过程中,求使点E到直线BC的距离等于3时对应的t的值.
【答案】(1)t=(6﹣2![]() )s时,P、E、C共线;(2)
)s时,P、E、C共线;(2)![]() 或4
或4![]() .
.
【解析】
(1)设AP=t,则PD=6﹣t,由点A、E关于直线BP对称,得出∠APB=∠BPE,由平行线的性质得出∠APB=∠PBC,得出∠BPC=∠PBC,在Rt△CDP中,由勾股定理得出方程,解方程即可得出结果;
(2)①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,AN=BM=![]() ,证出△BME∽△ENP,得出
,证出△BME∽△ENP,得出![]() ,求出NP=
,求出NP=![]() ,即可得出结果;
,即可得出结果;
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,则BH=3,BE=AB=4,AH=AB+BH=7,HE=![]() ,证得△AHE∽△PAB,得出
,证得△AHE∽△PAB,得出![]() ,即可得出结果.
,即可得出结果.
解:(1)设AP=t,则PD=6﹣t,如图1所示:
∵点A、E关于直线BP对称,
∴∠APB=∠BPE,
∵AD∥BC,
∴∠APB=∠PBC,
∵P、E、C共线,
∴∠BPC=∠PBC,
∴CP=BC=AD=6,
在Rt△CDP中,CD2+DP2=PC2,
即:42+(6﹣t)2=62,
解得:t=6﹣![]() 或6+
或6+![]() (不合题意舍去),
(不合题意舍去),
∴t=(6﹣![]() )s时,P、E、C共线;
)s时,P、E、C共线;
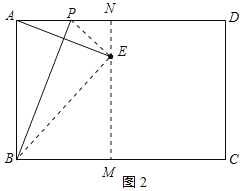
(2)①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,如图2所示:
则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,
在Rt△EBM中,AN=BM=![]() ,
,
∵点A、E关于直线BP对称,
∴∠PEB=∠PAB=90°,
∵∠ENP=∠EMB=∠PEB=90°,
∴∠PEN=∠EBM,
∴△BME∽△ENP,
∴![]() ,即
,即![]() ,
,
∴NP=![]() ,
,
∴t=AP=AN﹣NP=![]() ;
;
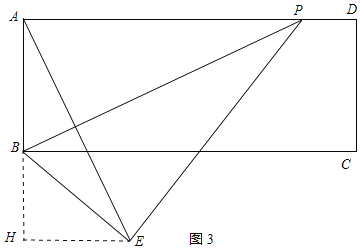
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,如图3所示:
则BH=3,BE=AB=4,AH=AB+BH=7,
在Rt△BHE中,HE=![]() ,
,
∵∠PAB=∠BHE=90°,AE⊥BP,
∴∠APB+∠EAP=∠HAE+∠EAP=90°,
∴∠HAE=∠APB,
∴△AHE∽△PAB,
∴![]() ,即
,即![]() ,
,
解得:t=AP=![]() ,
,
综上所述,t=![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庐阳春风体育运动品商店从厂家购进甲,乙两种T恤共400件,其每件的售价与进货量![]() (件)之间的关系及成本如下表所示:
(件)之间的关系及成本如下表所示:
T恤 | 每件的售价/元 | 每件的成本/元 |
甲 |
| 50 |
乙 |
| 60 |
|
(1)当甲种T恤进货250件时,求两种T恤全部售完的利润是多少元;
(2)若所有的T恤都能售完,求该商店获得的总利润![]() (元)与乙种T恤的进货量
(元)与乙种T恤的进货量![]() (件)之间的函数关系式;
(件)之间的函数关系式;
(3)在(2)的条件下,已知两种T恤进货量都不低于100件,且所进的T恤全部售完,该商店如何安排进货才能使获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
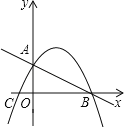
【题目】如图,直线y=﹣![]() x+2交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
x+2交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
(1)求抛物线的表达式;
(2)当点M在线段AB上方的曲线上移动时,求四边形AOBM的面积的最大值;
(3)点E在抛物线的对称轴上,点F在抛物线上,是否存在点F使得以A、C、E、F为顶点的四边形是平行四边形?若存在求出点F坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
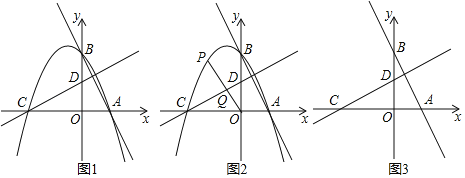
【题目】如图1,在平面直角坐标系中,直线AB:y=kx+b(k<0,b>0),与x轴交于点A、与y轴交于点B,直线CD与x轴交于点C、与y轴交于点D.若直线CD的解析式为y=﹣![]() (x+b),则称直线CD为直线AB的”姊线”,经过点A、B、C的抛物线称为直线AB的“母线”.
(x+b),则称直线CD为直线AB的”姊线”,经过点A、B、C的抛物线称为直线AB的“母线”.
(1)若直线AB的解析式为:y=﹣3x+6,求AB的”姊线”CD的解析式为: (直接填空);
(2)若直线AB的”母线”解析式为:![]() ,求AB的”姊线”CD的解析式;
,求AB的”姊线”CD的解析式;
(3)如图2,在(2)的条件下,点P为第二象限”母线”上的动点,连接OP,交”姊线”CD于点Q,设点P的横坐标为m,PQ与OQ的比值为y,求y与m的函数关系式,并求y的最大值;
(4)如图3,若AB的解析式为:y=mx+3(m<0),AB的“姊线”为CD,点G为AB的中点,点H为CD的中点,连接OH,若GH=![]() ,请直接写出AB的”母线”的函数解析式.
,请直接写出AB的”母线”的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车去上学途中,经过先上坡后下坡的一段路,在这段路上所骑行的路程![]() (米)与时间
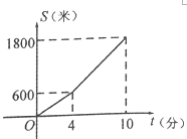
(米)与时间![]() (分钟)之间的函数关系如图所示.下列结论:①小明上学途中下坡路的长为1800米;②小明上学途中上坡速度为150米/分,下坡速度为200米/分;③如果小明放学后按原路返回,且往返过程中,上、下坡的速度都相同,则小明返回时经过这段路比上学时多用1分钟;④如果小明放学后按原路返回,返回所用时间与上学所用时间相等,且返回时下坡速度是上坡速度的1.5倍,则返回时上坡速度是160米/分其中正确的有( )
(分钟)之间的函数关系如图所示.下列结论:①小明上学途中下坡路的长为1800米;②小明上学途中上坡速度为150米/分,下坡速度为200米/分;③如果小明放学后按原路返回,且往返过程中,上、下坡的速度都相同,则小明返回时经过这段路比上学时多用1分钟;④如果小明放学后按原路返回,返回所用时间与上学所用时间相等,且返回时下坡速度是上坡速度的1.5倍,则返回时上坡速度是160米/分其中正确的有( )
A.①④B.②③C.②③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
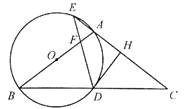
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的⊙
为直径的⊙![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若⊙![]() 的半径为4,①当
的半径为4,①当![]() 时,求
时,求![]() 的长(结果保留π);②当
的长(结果保留π);②当![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
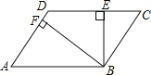
【题目】如图,平行四边形ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=2,DF=1,∠EBF=60°,则这个平行四边形ABCD的面积是( )
A. 2![]() B. 2
B. 2![]()
C. 3![]() D. 12
D. 12![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
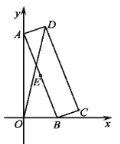
【题目】如图,矩形硬纸片ABCD的顶点A在![]() 轴的正半轴及原点上滑动,顶点B在
轴的正半轴及原点上滑动,顶点B在![]() 轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为
轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为![]() ,其中正确的结论是_________(填写序号).
,其中正确的结论是_________(填写序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com