
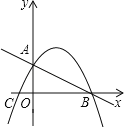
【题目】如图,直线y=﹣![]() x+2交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
x+2交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
(1)求抛物线的表达式;
(2)当点M在线段AB上方的曲线上移动时,求四边形AOBM的面积的最大值;
(3)点E在抛物线的对称轴上,点F在抛物线上,是否存在点F使得以A、C、E、F为顶点的四边形是平行四边形?若存在求出点F坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)当a=2时,S四边形AOBM的面积最大,为8;(3)存在.
;(2)当a=2时,S四边形AOBM的面积最大,为8;(3)存在.![]()
【解析】
(1)由直线y=﹣![]() x+2易确定A、B两点坐标,又由AC⊥AB则易证明△ACO∽△BOC,利用相似比可确定C点坐标,再利用待定系数法直接求解即可.
x+2易确定A、B两点坐标,又由AC⊥AB则易证明△ACO∽△BOC,利用相似比可确定C点坐标,再利用待定系数法直接求解即可.
(2)用待定系数法设出M点坐标和D点坐标,已表示出MD的长度为﹣![]() a2+4a,再利用割补法表示△AMB的面积,将得到的表达式转化为二次函数顶点式求解即可.
a2+4a,再利用割补法表示△AMB的面积,将得到的表达式转化为二次函数顶点式求解即可.
(3)利用平行四边形的性质分别作AC∥EF,AE∥CF两种情况的图形使E在抛物线对称轴上,F在抛物线上,利用待定系数法及图形的性质求解即可.
解:(1)∵直线y=﹣![]() x+2交x轴于A、B两点
x+2交x轴于A、B两点
∴A(0,2)、B(4,0)
由AC⊥AB得,△AOC∽△BOA.
∴![]() .
.
∴OC=1.
又∵C在x轴负半轴上
∴C(﹣1,0).
设抛物线解析式y=ax2+bx+c.
把A(0,2),B(4,0),C(﹣1,0)代入上式得,
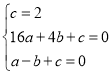 ,解得,
,解得,
∴抛物线解析式为,y=![]() .
.
(2)如图1,
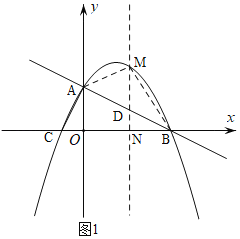
过点M作MN⊥x轴,交直线AB与点D.
设M点横坐标为a,则M(a, ![]() ),D(a,
),D(a,![]() )
)
∴MD=![]() ﹣(
﹣(![]() )=
)=![]()
∴S△ABM=![]() MDBO=
MDBO=![]() (﹣
(﹣![]() a2+2a)4=﹣a2+4a
a2+2a)4=﹣a2+4a
∴S四边形AOBM=﹣a2+4a+![]() ×2×4=﹣(a﹣2)2+8
×2×4=﹣(a﹣2)2+8
故当a=2时,S四边形AOBM的面积最大,为8.
(3)存在.
如图2﹣1,
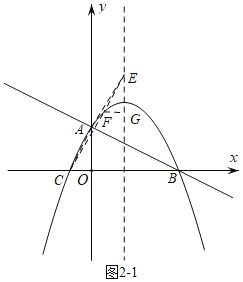
当AC∥EF,F在对称轴左侧时,可以看作把△AOC沿水平向右平移至OA与对称轴重合时,再将其向上平移,恰好使点A与点E重合,点C与点F重合.
此时四边形ACFE为平行四边形.
∴FD=OC=1.
∴点F的横坐标为,x=![]() .
.
当x=![]() 时,y=﹣
时,y=﹣![]() ×(
×(![]() )2+
)2+![]() ×
×![]() +2=
+2=![]() .
.
即此时F(![]() ,
,![]() ).
).
如图2﹣2,

当AC∥EF,F在对称轴右侧时,把△EFG绕点G旋转180°恰好与抛物线相交于F,则四边形ACEF为平行四边形.
此时易得F点纵坐标为,y=![]() .
.
当y=![]() 时,﹣
时,﹣![]() x2+
x2+![]() x+2=0.
x+2=0.
解得,x=![]() (舍去)或x=
(舍去)或x=![]() .
.
此时F(![]() ,
,![]() ).
).
如图2﹣3,
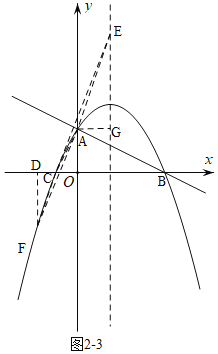
以线段AC为对角线作AECF,过A作AG垂直于对称轴直线于点G.过点F作FD⊥x轴交于点D.
∴AG=1.5
又∵△AGE≌△CDF
∴CD=1.5
∴D点坐标为(﹣2.5,0)
∴当x=﹣2.5时,y=﹣![]() ×(﹣
×(﹣![]() )2+
)2+![]() ×(﹣
×(﹣![]() )+2=﹣
)+2=﹣![]()
∴此时F(﹣![]() ,﹣
,﹣![]() ).
).
综上所述,满足题意的F点坐标有,(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(﹣
),(﹣![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】 如图,P为平行四边形ABCD的边AD上的任意一点,E,F分别为PB,PC的中点,四边形BCFE,△PDC,△PAB的面积分别为S,S1,S2,若S=12,则S1+S2的值为( )
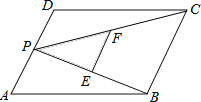
A. 12B. 14C. 16D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,某校学生会为了调查学生对雾霾天气知识的了解程度,随机抽取了该校的n名学生做了一次跟踪调查,将调查结果分为四个等级:(A)非常了解.(B)比较了解.(C)基本了解.(D)不了解,并将调查结果绘制成如下两幅不完整统计图.
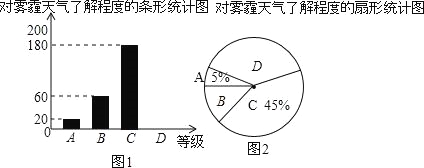
根据统计图提供的信息,解答下列问题:
(1)求n的值;
(2)在调查的n名学生中,对雾霾天气知识不了解的学生有 人,并将条形统计图补充完整.
(3)估计该校1500名学生中,对雾霾天气知识比较了解的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.
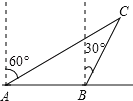
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线DE交x轴于点E(30,0),交y轴于点D(0,40),直线AB:y=![]() x+5交x轴于点A,交y轴于点B,交直线DE于点P,过点E作EF⊥x轴交直线AB于点F,以EF为一边向右作正方形EFGH.
x+5交x轴于点A,交y轴于点B,交直线DE于点P,过点E作EF⊥x轴交直线AB于点F,以EF为一边向右作正方形EFGH.
(1)求边EF的长;
(2)将正方形EFGH沿射线FB的方向以每秒![]() 个单位的速度匀速平移,得到正方形E1F1G1H1,在平移过程中边F1G1始终与y轴垂直,设平移的时间为t秒(t>0).
个单位的速度匀速平移,得到正方形E1F1G1H1,在平移过程中边F1G1始终与y轴垂直,设平移的时间为t秒(t>0).
①当点F1移动到点B时,求t的值;
②当G1,H1两点中有一点移动到直线DE上时,请直接写出此时正方形E1F1G1H1与△APE重叠部分的面积.
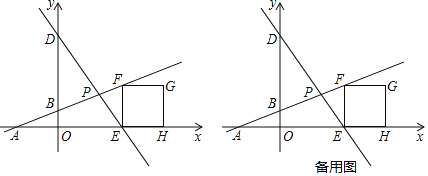
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=4,动点P从点A出发,沿AD方向以每秒1个单位的速度运动,连接BP,作点A关于直线BP的对称点E,设点P的运动时间为t(s).
(1)若AD=6,P仅在边AD运动,求当P,E,C三点在同一直线上时对应的t的值.
(2)在动点P在射线AD上运动的过程中,求使点E到直线BC的距离等于3时对应的t的值.
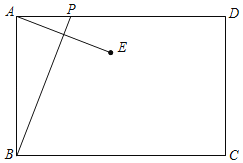
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条长1200 m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把直线y=﹣2x向上平移后,分别交y轴、x轴于A、B两点,直线AB经过点(m,n)且2m+n=6,则点O到线段AB的距离为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com