
【题目】 如图,P为平行四边形ABCD的边AD上的任意一点,E,F分别为PB,PC的中点,四边形BCFE,△PDC,△PAB的面积分别为S,S1,S2,若S=12,则S1+S2的值为( )
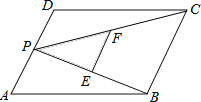
A. 12B. 14C. 16D. 18
【答案】C
【解析】
先根据平行四边形与中位线定理求出EF=![]() BC,再得出△PEF∽△PBC,且相似比为1:2,求得S△PEF=4,再求出S△PBC的面积.
BC,再得出△PEF∽△PBC,且相似比为1:2,求得S△PEF=4,再求出S△PBC的面积.
解:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,EF=![]() BC,
BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=![]() =1:4,S四边形BCFE=12,
=1:4,S四边形BCFE=12,
∴S△PEF=4,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=16.
故选:C.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解我市居民的低碳生活状况,适宜采用抽样调查的方法
B. 一组数据2,2,3,6的众数和中位数都是2
C. “掷一枚硬币正面朝上的概率是![]() ”,表示每抛硬币2次就有1次正面朝上
”,表示每抛硬币2次就有1次正面朝上
D. 随机抽取甲乙两名同学的5次数学成绩,平均分都是90分,方差分别是S甲2=5,S乙2=10,说明乙的成绩较为稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂准备生产甲、乙两种商品销往“一带一路”沿线国家和地区.已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.求甲种商品与乙种商品的销售单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,将边AB绕点A顺时针旋转60°得到线段AD,将边AC绕点A逆时针旋转120°得到线段AE,连接DE.
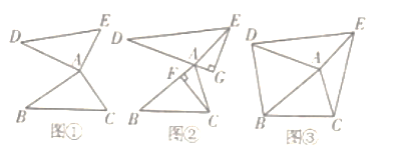
(1)、如图①,当∠BAC=90°时,若△ABC的面积为5,则△ADE的面积为________;
(2)如图②,CF、BG分别是△ABC和△ADE的高,若△ABC为任意三角形,△ABC与△ADE的面积是否相等,请说明理由;
(3)如图③,连接BD、CE.若AB=4,AC=2![]() ,四边形CEDB的面积为13
,四边形CEDB的面积为13![]() ,则△ABC的面积为________.
,则△ABC的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.

(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
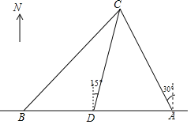
【题目】“仁爱礁”自古以来就是中国固有领海,也是中国渔民的传统渔场.为了维护我国渔民合法的海洋权益,每年我“渔政海巡船”都到“仁爱礁”进行护渔活动.如图,在岛礁东西方向上,有A,B两艘渔政船,现均收到我故障渔船C的求救信号.已知A,B两船相距90(![]() +1)海里,渔船C在船A的北偏西30°方向上,渔船C在船B的东北方向上,岛礁上有一观测点D,测得船C正好在观测点D的北偏东15°方向上
+1)海里,渔船C在船A的北偏西30°方向上,渔船C在船B的东北方向上,岛礁上有一观测点D,测得船C正好在观测点D的北偏东15°方向上
(1)分别求出AC和AD距离(若结果有根号,请保留根号);
(2)已知距观测点D处110海里范围内有暗礁.为了及时营救渔船C,决定让海巡船A去营救,若海巡船A沿直线AC去营救,途中有无触暗礁危险?请说明理由:(参考数据:![]() ≈141,
≈141,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
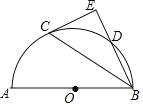
【题目】如图,点D是以AB为直径的半圆O上一点,连接BD,点C是![]() 的中点,过点C作直线BD的垂线,垂足为点E.
的中点,过点C作直线BD的垂线,垂足为点E.
求证:(1)CE是半圆O的切线;
(2)BC2=ABBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
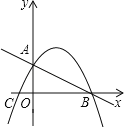
【题目】如图,直线y=﹣![]() x+2交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
x+2交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
(1)求抛物线的表达式;
(2)当点M在线段AB上方的曲线上移动时,求四边形AOBM的面积的最大值;
(3)点E在抛物线的对称轴上,点F在抛物线上,是否存在点F使得以A、C、E、F为顶点的四边形是平行四边形?若存在求出点F坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com