
【题目】在△ABC中,将边AB绕点A顺时针旋转60°得到线段AD,将边AC绕点A逆时针旋转120°得到线段AE,连接DE.
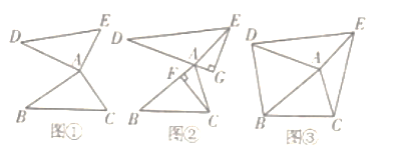
(1)、如图①,当∠BAC=90°时,若△ABC的面积为5,则△ADE的面积为________;
(2)如图②,CF、BG分别是△ABC和△ADE的高,若△ABC为任意三角形,△ABC与△ADE的面积是否相等,请说明理由;
(3)如图③,连接BD、CE.若AB=4,AC=2![]() ,四边形CEDB的面积为13
,四边形CEDB的面积为13![]() ,则△ABC的面积为________.
,则△ABC的面积为________.
【答案】(1)5;(2)相等,理由见解析;(3)![]()
【解析】
(1)继而得∠DAE=∠BAC=90°,可证得△ABC≌△ADE,则两三角形面积相等;
(2)由∠BAD=60°,∠CAE=120°得∠DAE+∠CAB=180°,根据平角定义可得∠DAE +∠GAE=180°,可得∠FAC=∠GAE,然后证得 △ACF≌△AEG,继而得CF=BG,根据等底等高的两个三角形面积相等可求出结论;
(3)如图,分别作出△ABD和△AEC的高AH,AF. 求得等边三角形△ABD的面积为4![]() 和△AECDE的面积3
和△AECDE的面积3![]() , 则△ADE和△ABC的面积之和为6
, 则△ADE和△ABC的面积之和为6![]() , 再证得 △ABC≌△ADE,从而证得△ADE和△ABC的面积都是3
, 再证得 △ABC≌△ADE,从而证得△ADE和△ABC的面积都是3![]() .
.
(1)根据旋转的性质可得AC=AE,AB=AD,∠BAD=60°,∠CAE=120°,
∵∠BAC=90°
∴∠DAE=90°
∴∠BAC=∠DAE
∴△ABC≌△ADE,
∵△ABC的面积为5
∴△ADE的面积为5.
(2)解:相等,
理由如下:
由旋转,得AC=AE,AB=AD,∠BAD=60°,∠CAE=120°,
∴∠BAD+∠CAE=180°,
∴∠DAE+∠CAB=180°,
∵∠DAE +∠GAE=180°,
∴∠FAC=∠GAE.
∵CF、BG分别是△ABC和△ADE的高,
∴∠AFC=∠AGE =90°,
∴△ACF≌△AEG,
∴CF=BG,
∴△ABC与△ADE的面积相等.
(3)如图,分别作出△ABD和△AEC的高AH,AF.
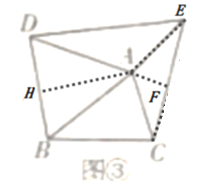
∵AC=AE,∠BAD=60°,
∴△ABD是等边三角形,
∴AH=![]() ,
,
∴S△ABD=![]() ,
,
同理可得S△AEC=3![]() ,
,
∴S△ADE+S△ABC=S四边形CEDB- S△ABD-S△AEC=6![]()
又△ABC≌△ADE,
∴S△ADE=3![]() .
.


科目:初中数学 来源: 题型:
【题目】某化工材料经销公司购进一种化工材料若干千克,价格为每千克40元,物价部门规定其销售单价不高于每千克70元,不低于每千克40元.经市场调查发现,日销量y(千克)是销售单价x(元)的一次函数,且当x=70时,y=80;x=60时,y=100.在销售过程中,每天还要支付其他费用350元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式;
(3)当销售单价为多少元时,该公司日获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
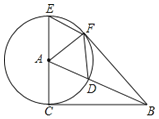
【题目】如图,在![]() △ABC中,∠ACB=
△ABC中,∠ACB=![]() ,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF,交⊙A于点F,连接AF,BF,DF.
,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF,交⊙A于点F,连接AF,BF,DF.
(1)求证:BF是⊙A的切线;
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给与证明.
(3)若EF=1,AE=2,求cos∠CBA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国诗词大会》栏目中,外卖小哥击败北大硕士引发新一轮中华优秀传统文化热。某文化中心开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》、《孟子》(依次用字母A,B,C,D分别表示这四个材料),将A,B,C.D分别写在4张完全相同的不适明卡片的正面,背面朝上洗匀后放在桌面上,比赛时甲选手先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由乙选手从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.用画树状图或列表的方法求他俩诵读两个不同材料的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
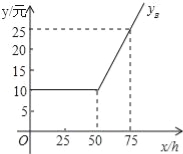
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,P为平行四边形ABCD的边AD上的任意一点,E,F分别为PB,PC的中点,四边形BCFE,△PDC,△PAB的面积分别为S,S1,S2,若S=12,则S1+S2的值为( )
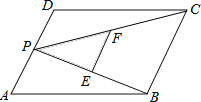
A. 12B. 14C. 16D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】咸宁市某中学为了解本校学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,随机抽取了部分学生进行问卷调查,根据调查结果绘制了如下图所示的两幅不完整统计图,请你根据图中信息解答下列问题:

⑴补全条形统计图,“体育”对应扇形的圆心角是 度;
⑵根据以上统计分析,估计该校![]() 名学生中喜爱“娱乐”的有 人;
名学生中喜爱“娱乐”的有 人;
⑶在此次问卷调查中,甲、乙两班分别有![]() 人喜爱新闻节目,若从这
人喜爱新闻节目,若从这![]() 人中随机抽取
人中随机抽取![]() 人去参加“新闻小记者”培训,请用列表法或者画树状图的方法求所抽取的
人去参加“新闻小记者”培训,请用列表法或者画树状图的方法求所抽取的![]() 人来自不同班级的概率
人来自不同班级的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
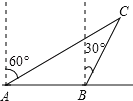
【题目】如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com