
【题目】如图,在![]() △ABC中,∠ACB=
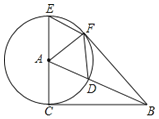
△ABC中,∠ACB=![]() ,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF,交⊙A于点F,连接AF,BF,DF.
,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF,交⊙A于点F,连接AF,BF,DF.
(1)求证:BF是⊙A的切线;
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给与证明.
(3)若EF=1,AE=2,求cos∠CBA的值.
【答案】(1)见解析;(2)∠CAB=![]() ,四边形ADFE为菱形,理由见解析.(3)
,四边形ADFE为菱形,理由见解析.(3)![]()
【解析】
(1)根据平行线的性质得∠E=∠CAB,∠EFA=∠FAB,加上∠E=∠EFA,则∠FAB=∠CAB,于是可判断△ABC≌△ABF,从而得到∠AFB=90°,然后根据切线的判定方法可判断BF是⊙A的切线;
(2)当∠CAB=60°,则∠FAB=∠EAF=60°,于是可证△AEF和△ADF都为等边三角形,所以AE=EF=AD=DF,然后根据菱形的判定方法可判断此时四边形ADFE是菱形;
(3)连接FC,证明∠ACF=∠CBA即可.
(1)证明:∵EF∥AB,
∴∠E=∠CAB,∠EFA=∠FAB,
∵∠E=∠EFA,
∴∠FAB=∠CAB,
在△ABC和△ABF中,
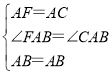 ,
,
∴△ABC≌△ABF(SAS),
∴∠AFB=∠ACB=90°,
∴BF⊥AF,
∵AF是⊙A的半径,
∴BF是⊙A的切线;
(2)解:当∠CAB=60°时,四边形ADFE为菱形.
理由如下:∵∠CAB=60°,
∴∠FAB=∠EAF=60°,
∵AE=AF=AD,
∴△AEF和△ADF都为等边三角形,
∴AE=EF=AD=DF,
∴四边形ADFE是菱形.
(3)连FC,

∵EC为直径,
∴∠EFC=90°
∵EF=1,AE=2,
∴FC=![]() ,
,
∵A为EC的中点,EF∥AB,
∴AB垂直平分线FC,交AB于P,则CP= ![]()
又∠ABC=∠ACP
cos∠ABC=![]() ∠ACP=
∠ACP=![]() =
=![]()


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
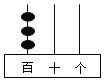
【题目】把3颗算珠放在计数器的3根插棒上构成一个数字,例如,如图摆放的算珠表示数300.现将3颗算珠任意摆放在这3根插棒上.
(1)若构成的数是两位数,则十位数字为1的概率为 ;
(2)求构成的数是三位数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解我市居民的低碳生活状况,适宜采用抽样调查的方法
B. 一组数据2,2,3,6的众数和中位数都是2
C. “掷一枚硬币正面朝上的概率是![]() ”,表示每抛硬币2次就有1次正面朝上
”,表示每抛硬币2次就有1次正面朝上
D. 随机抽取甲乙两名同学的5次数学成绩,平均分都是90分,方差分别是S甲2=5,S乙2=10,说明乙的成绩较为稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
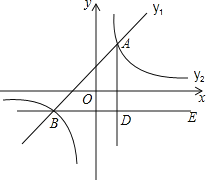
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 请直接写出
请直接写出![]() 时,x的取值范围;
时,x的取值范围;
![]() 过点B作
过点B作![]() 轴,
轴,![]() 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为监控某条生产线上产品的质量,检测员每个相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的个数据按从小到大的顺序整理成如下表格:
编号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ | |||||
尺寸(cm) | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 | a | 9.03 | 9.04 | 9.06 | 9.07 | 9.08 | b |
按照生产标准,产品等次规定如下:
尺寸(单位:cm) | 产品等次 |
8.97≤x≤9.03 | 特等品 |
8.95≤x≤9.05 | 优等品 |
8.90≤x≤9.10 | 合格品 |
x<8.90或x>9.10 | 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)仅算在内.
(1)已知此次抽检的合格率为80%,请判断编号为的产品是否为合格品,并说明理由
(2)已知此次抽检出的优等品尺寸的中位数为9cm.
(i)求a的值,
(ii)将这些优等品分成两组,一组尺寸大于9cm,另一组尺寸不大于9cm,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新园小区计划在一块长为20米,宽12米的矩形场地上修建三条互相垂直的长方形甬路(一条橫向、两条纵向,且横向、纵向的宽度比为3:2),其余部分种花草.若要使种花草的面积达到144米2.则横向的甬路宽为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂准备生产甲、乙两种商品销往“一带一路”沿线国家和地区.已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.求甲种商品与乙种商品的销售单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,将边AB绕点A顺时针旋转60°得到线段AD,将边AC绕点A逆时针旋转120°得到线段AE,连接DE.
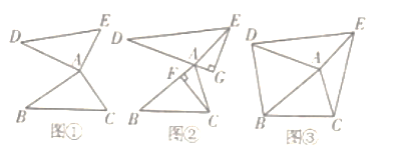
(1)、如图①,当∠BAC=90°时,若△ABC的面积为5,则△ADE的面积为________;
(2)如图②,CF、BG分别是△ABC和△ADE的高,若△ABC为任意三角形,△ABC与△ADE的面积是否相等,请说明理由;
(3)如图③,连接BD、CE.若AB=4,AC=2![]() ,四边形CEDB的面积为13
,四边形CEDB的面积为13![]() ,则△ABC的面积为________.
,则△ABC的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
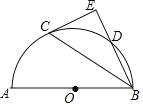
【题目】如图,点D是以AB为直径的半圆O上一点,连接BD,点C是![]() 的中点,过点C作直线BD的垂线,垂足为点E.
的中点,过点C作直线BD的垂线,垂足为点E.
求证:(1)CE是半圆O的切线;
(2)BC2=ABBE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com