
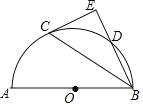
【题目】如图,点D是以AB为直径的半圆O上一点,连接BD,点C是![]() 的中点,过点C作直线BD的垂线,垂足为点E.
的中点,过点C作直线BD的垂线,垂足为点E.
求证:(1)CE是半圆O的切线;
(2)BC2=ABBE.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)连接OC,根据圆周角定理得到∠ABC=∠DBC,根据等腰三角形的性质得到∠OCB=∠OBC,等量代换得到∠OCB=∠CBD,推出OC∥BD,根据平行线的性质得到OC⊥CE,于是得到结论;
(2)连接AC,由AB是⊙O的直径,得到∠ACB=90°,根据相似三角形的性质即可得到结论.
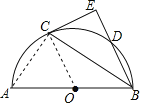
证明:(1)连接OC,
∵点C是![]() 的中点,
的中点,
∴![]() ,
,
∴∠ABC=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OCB=∠CBD,
∴OC∥BD,
∵CE⊥BE,
∴OC⊥CE,
∴CE是半圆O的切线;
(2)连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CE⊥BE,
∴∠E=90°,
∴∠E=∠ACB,
∵∠ABC=∠CBD,
∴△ABC∽△CBE,
∴![]() ,
,
∴BC2=ABBE.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() △ABC中,∠ACB=
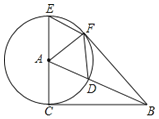
△ABC中,∠ACB=![]() ,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF,交⊙A于点F,连接AF,BF,DF.
,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF,交⊙A于点F,连接AF,BF,DF.
(1)求证:BF是⊙A的切线;
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给与证明.
(3)若EF=1,AE=2,求cos∠CBA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
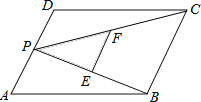
【题目】 如图,P为平行四边形ABCD的边AD上的任意一点,E,F分别为PB,PC的中点,四边形BCFE,△PDC,△PAB的面积分别为S,S1,S2,若S=12,则S1+S2的值为( )
A. 12B. 14C. 16D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】咸宁市某中学为了解本校学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,随机抽取了部分学生进行问卷调查,根据调查结果绘制了如下图所示的两幅不完整统计图,请你根据图中信息解答下列问题:

⑴补全条形统计图,“体育”对应扇形的圆心角是 度;
⑵根据以上统计分析,估计该校![]() 名学生中喜爱“娱乐”的有 人;
名学生中喜爱“娱乐”的有 人;
⑶在此次问卷调查中,甲、乙两班分别有![]() 人喜爱新闻节目,若从这
人喜爱新闻节目,若从这![]() 人中随机抽取
人中随机抽取![]() 人去参加“新闻小记者”培训,请用列表法或者画树状图的方法求所抽取的
人去参加“新闻小记者”培训,请用列表法或者画树状图的方法求所抽取的![]() 人来自不同班级的概率
人来自不同班级的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
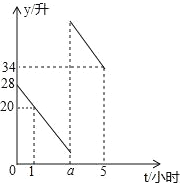
(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,某校学生会为了调查学生对雾霾天气知识的了解程度,随机抽取了该校的n名学生做了一次跟踪调查,将调查结果分为四个等级:(A)非常了解.(B)比较了解.(C)基本了解.(D)不了解,并将调查结果绘制成如下两幅不完整统计图.
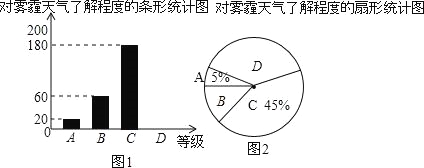
根据统计图提供的信息,解答下列问题:
(1)求n的值;
(2)在调查的n名学生中,对雾霾天气知识不了解的学生有 人,并将条形统计图补充完整.
(3)估计该校1500名学生中,对雾霾天气知识比较了解的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.
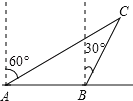
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条长1200 m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com