
【题目】如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=_____.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】新园小区计划在一块长为20米,宽12米的矩形场地上修建三条互相垂直的长方形甬路(一条橫向、两条纵向,且横向、纵向的宽度比为3:2),其余部分种花草.若要使种花草的面积达到144米2.则横向的甬路宽为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
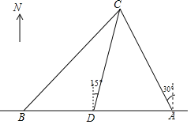
【题目】“仁爱礁”自古以来就是中国固有领海,也是中国渔民的传统渔场.为了维护我国渔民合法的海洋权益,每年我“渔政海巡船”都到“仁爱礁”进行护渔活动.如图,在岛礁东西方向上,有A,B两艘渔政船,现均收到我故障渔船C的求救信号.已知A,B两船相距90(![]() +1)海里,渔船C在船A的北偏西30°方向上,渔船C在船B的东北方向上,岛礁上有一观测点D,测得船C正好在观测点D的北偏东15°方向上
+1)海里,渔船C在船A的北偏西30°方向上,渔船C在船B的东北方向上,岛礁上有一观测点D,测得船C正好在观测点D的北偏东15°方向上
(1)分别求出AC和AD距离(若结果有根号,请保留根号);
(2)已知距观测点D处110海里范围内有暗礁.为了及时营救渔船C,决定让海巡船A去营救,若海巡船A沿直线AC去营救,途中有无触暗礁危险?请说明理由:(参考数据:![]() ≈141,
≈141,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
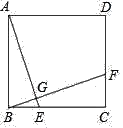
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
查看答案和解析>>
科目:初中数学 来源: 题型:
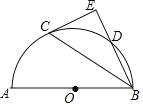
【题目】如图,点D是以AB为直径的半圆O上一点,连接BD,点C是![]() 的中点,过点C作直线BD的垂线,垂足为点E.
的中点,过点C作直线BD的垂线,垂足为点E.
求证:(1)CE是半圆O的切线;
(2)BC2=ABBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
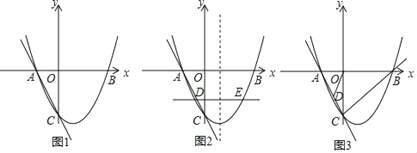
(1)求直线AC的解析式;
(2)如图2,点E(a,b)是对称轴右侧抛物线上一点,过点E垂直于y轴的直线与AC交于点D(m,n).点P是x轴上的一点,点Q是该抛物线对称轴上的一点,当a+m最大时,求点E的坐标,并直接写出EQ+PQ+![]() PB的最小值;
PB的最小值;
(3)如图3,在(2)的条件下,连结OD,将△AOD沿x轴翻折得到△AOM,再将△AOM沿射线CB的方向以每秒3个单位的速度沿平移,记平移后的△AOM为△A′O'M',同时抛物线以每秒1个单位的速度沿x轴正方向平移,点B的对应点为B'.△A'B'M'能否为等腰三角形?若能,请求出所有符合条件的点M'的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料69千克,乙种原料52千克,现计划用这两种原料生产A,B两种型号的产品共80件,已知每件A型号产品需要甲种原料0.6千克,乙种原料0.9千克;每件B型号产品需要甲种原料1.1千克,乙种原料0.4千克.请解答下列问题:
(1)该工厂有哪几种生产方案?
(2)在这批产品全部售出的条件下,若1件A型号产品获利35元,1件B型号产品获利25元,(1)中哪种方案获利最大?最大利润是多少?
(3)在(2)的条件下,工厂决定将所有利润的25%全部用于再次购进甲、乙两种原料,要求每种原料至少购进4千克,且购进每种原料的数量均为整数.若甲种原料每千克40元,乙种原料每千克60元,请直接写出购买甲、乙两种原料之和最多的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某特产店出售大米,一天可销售20袋,每袋可盈利40元,为了扩大销售,增加盈利,尽快减少库存,决定采取降价措施,据统计发现,若每袋降价2元,平均每天可多售4袋.
(1)设每袋大米降价为x(x为偶数)元时,利润为y元,写出y与x的函数关系式.
(2)若每天盈利1200元,则每袋应降价多少元?
(3)每袋大米降价多少元时,商店可获最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com