
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
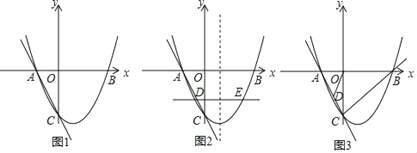
(1)求直线AC的解析式;
(2)如图2,点E(a,b)是对称轴右侧抛物线上一点,过点E垂直于y轴的直线与AC交于点D(m,n).点P是x轴上的一点,点Q是该抛物线对称轴上的一点,当a+m最大时,求点E的坐标,并直接写出EQ+PQ+![]() PB的最小值;
PB的最小值;
(3)如图3,在(2)的条件下,连结OD,将△AOD沿x轴翻折得到△AOM,再将△AOM沿射线CB的方向以每秒3个单位的速度沿平移,记平移后的△AOM为△A′O'M',同时抛物线以每秒1个单位的速度沿x轴正方向平移,点B的对应点为B'.△A'B'M'能否为等腰三角形?若能,请求出所有符合条件的点M'的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)E(3,
;(2)E(3,![]() ),点F(﹣1,
),点F(﹣1,![]() ),
),![]() ;(3)符合条件的点M'的坐标M′(0,
;(3)符合条件的点M'的坐标M′(0,![]() ).
).
【解析】
(1)y=![]() ,令y=0,x=0,求出A(﹣2,0)、B(4,0)、C(0,﹣2
,令y=0,x=0,求出A(﹣2,0)、B(4,0)、C(0,﹣2![]() ),把A、C坐标代入y=kx+b,即可求解;
),把A、C坐标代入y=kx+b,即可求解;
(2)①由n=b,解得:m=﹣![]() m2+
m2+![]() a,则a+m=a+(﹣
a,则a+m=a+(﹣![]() m2+
m2+![]() a)=﹣
a)=﹣![]() (a﹣3)2+
(a﹣3)2+![]() ,即可求解;②F是E关于对称轴的对称点,则在如图位置时,EQ+PQ=PF最小,即EQ+PQ+
,即可求解;②F是E关于对称轴的对称点,则在如图位置时,EQ+PQ=PF最小,即EQ+PQ+![]() PB是最小值,即可求解;
PB是最小值,即可求解;
(3)设移动的时间t秒,各点坐标为:A′(﹣2+2t)、B′(4+t)、M′(﹣![]() +2t,
+2t,![]() t),分AB′2=AM′2、AB′2=BM′2、BM′2=AM′2讨论求解.
t),分AB′2=AM′2、AB′2=BM′2、BM′2=AM′2讨论求解.
(1)y=![]() ,
,
令y=0,解得x=﹣2或4,令x=0,则y=﹣2![]() ,
,
∴点A(﹣2,0)、B(4,0)、C(0,﹣2![]() );
);
把A、C坐标代入y=kx+b,
解得:k=﹣![]() ,b=﹣2
,b=﹣2![]() ,
,
∴直线AC的解析式y=﹣![]() x﹣2
x﹣2![]() ;
;
(2)∵E(a,b)在抛物线上,∴b=![]() ,
,
∵D(m,n)在直线AC上,∴n=﹣![]() m﹣2
m﹣2![]() ,
,
∵DE⊥y轴,∴n=b,解得:m=﹣![]() a2+
a2+![]() a,
a,
∴a+m=a+(﹣![]() a2+
a2+![]() a)=﹣
a)=﹣![]() (a﹣3)2+
(a﹣3)2+![]() ,
,
∴当a=3时,a+m由最大值,b=![]() ,
,
则:E(3,![]() ),点F(﹣1,
),点F(﹣1,![]() ),
),
如下图2所示,连接BC,过点F作FP∥BC,交对称轴和x轴于点Q、P,
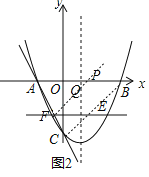
∵F是E关于对称轴的对称点,则在如图位置时,EQ+PQ=PF最小,即EQ+PQ+![]() PB是最小值,
PB是最小值,
kBC=![]() =kFP,把kFP和点F坐标代入y=kx+b,
=kFP,把kFP和点F坐标代入y=kx+b,
解得:b=﹣![]() ,即:y=
,即:y=![]() x﹣
x﹣![]() ,
,
令y=0,则x=![]() ,即点P(
,即点P(![]() ,0),
,0),
则PF=![]() ,而
,而![]() PB=
PB=![]() (4﹣
(4﹣![]() )=
)=![]() ,
,
EQ+PQ+![]() PB=PF+
PB=PF+![]() PB=
PB=![]() ;
;
故:点E坐标为(3,![]() ),EQ+PQ+
),EQ+PQ+![]() PB的最小值为
PB的最小值为![]() ;
;
(3)设移动的时间t秒,△A′O′M′移动到如图所示的位置,
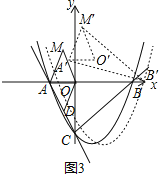
则此时各点坐标为:A′(﹣2+2t)、B′(4+t)、M′(﹣![]() +2t,
+2t,![]() +
+![]() t),
t),
则AB′2=6t2﹣12t+36,AM′2=![]() ,BM′2=6t2+3t+
,BM′2=6t2+3t+![]() ,
,
当AB′2=AM′2时,6t2﹣12t+36=![]() ,方程无解,
,方程无解,
当AB′2=BM′2时,6t2﹣12t+36=6t2+3t+![]() ,t=
,t=![]() ,M′(0,
,M′(0,![]() ),
),
当BM′2=AM′2时,6t2+3t+![]() =
=![]() ,方程无解,
,方程无解,
故:符合条件的点M'的坐标M′(0,![]() ).
).


科目:初中数学 来源: 题型:
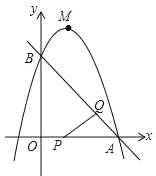
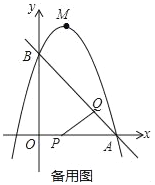
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
(1)求抛物线的解析式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
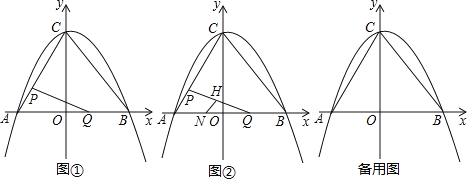
【题目】如图①,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图②,点N的坐标为(﹣![]() ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为参加11月23日举行的丹东市“我爱诗词”中小学生诗词大赛决赛,某校每班选25名同学参加预选赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为10分、9分、8分、7分,学校将八年级的一班和二班的成绩整理并绘制成如下统计图:

根据以上提供的信息解答下列问题
(1)请补全一班竞赛成绩统计图;
(2)请直接写出a、b、c、d的值;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
一班 | a= | b= | 9 |
二班 | 8.76 | c= | d= |
(3)请从平均数和中位数两个方面对这两个班级的成绩进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数y=-![]() 和y=
和y=![]() 的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .
的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com