
ЁОЬтФПЁПФГЛЏЙЄВФСЯОЯњЙЋЫОЙКНјвЛжжЛЏЙЄВФСЯШєИЩЧЇПЫЃЌМлИёЮЊУПЧЇПЫ40дЊЃЌЮяМлВПУХЙцЖЈЦфЯњЪлЕЅМлВЛИпгкУПЧЇПЫ70дЊЃЌВЛЕЭгкУПЧЇПЫ40дЊЃЎОЪаГЁЕїВщЗЂЯжЃЌШеЯњСПy(ЧЇПЫ)ЪЧЯњЪлЕЅМлx(дЊ)ЕФвЛДЮКЏЪ§ЃЌЧвЕБxЃН70ЪБЃЌyЃН80ЃЛxЃН60ЪБЃЌyЃН100ЃЎдкЯњЪлЙ§ГЬжаЃЌУПЬьЛЙвЊжЇИЖЦфЫћЗбгУ350дЊЃЎ
(1)ЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
(2)ЧѓИУЙЋЫОЯњЪлИУдСЯШеЛёРћw(дЊ)гыЯњЪлЕЅМлx(дЊ)жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌИУЙЋЫОШеЛёРћзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЁОД№АИЁП(1) yЃНЉ2x+220(40ЁмxЁм70)ЃЛ(2) wЃНЉ2x2+300xЉ9150ЃЛ(3) ЕБЯњЪлЕЅМлЮЊ70дЊЪБЃЌИУЙЋЫОШеЛёРћзюДѓЃЌЮЊ2050дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнyгыxГЩвЛДЮКЏЪ§НтЮіЪНЃЌЩшЮЊyЃНkx+bЃЈkЁй0ЃЉЃЌАбxгыyЕФСНЖджЕДњШыЧѓГіkгыbЕФжЕЃЌМДПЩШЗЖЈГіyгыxЕФНтЮіЪНЃЌВЂЧѓГіxЕФЗЖЮЇМДПЩЃЛ
ЃЈ2ЃЉИљОнРћШѓЃНЕЅМлЁСЯњЪлСПЃЌСаГіwЙигкxЕФЖўДЮКЏЪ§НтЮіЪНМДПЩЃЛ
ЃЈ3ЃЉРћгУЖўДЮКЏЪ§ЕФаджЪЧѓГіwЕФзюДѓжЕЃЌвдМАДЫЪБxЕФжЕМДПЩЃЎ
(1)ЩшyЃНkx+b(kЁй0)ЃЌ
ИљОнЬтвтЕУ![]() ЃЌ
ЃЌ
НтЕУЃКkЃНЉ2ЃЌbЃН220ЃЌ
ЁрyЃНЉ2x+220(40ЁмxЁм70)ЃЛ
(2)wЃН(xЉ40)(Љ2x+220)Љ350ЃНЉ2x2+300xЉ9150ЃНЉ2(xЉ75)2+2100ЃЛ
(3)wЃНЉ2(xЉ75)2+2100ЃЌ
Ёп40ЁмxЁм70ЃЌ
ЁрxЃН70ЪБЃЌwгазюДѓжЕЮЊwЃНЉ2ЁС25+2100ЃН2050дЊЃЌ
ЁрЕБЯњЪлЕЅМлЮЊ70дЊЪБЃЌИУЙЋЫОШеЛёРћзюДѓЃЌЮЊ2050дЊЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
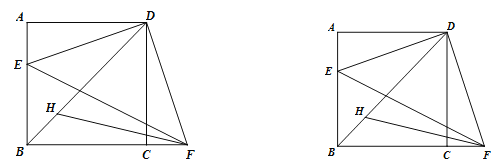
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЪЧБпABЩЯЕФвЛЖЏЕуЃЌЕуFдкБпBCЕФбгГЄЯпЩЯЃЌЧв![]() ЃЌСЌНгDEЃЌDFЃЌEF. FHЦНЗж
ЃЌСЌНгDEЃЌDFЃЌEF. FHЦНЗж![]() НЛBDгкЕуH.
НЛBDгкЕуH.
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃК
ЃК
ЃЈ3ЃЉЙ§ЕуHзї![]() гкЕуMЃЌгУЕШЪНБэЪОЯпЖЮABЃЌHMгыEFжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУї.
гкЕуMЃЌгУЕШЪНБэЪОЯпЖЮABЃЌHMгыEFжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУї.
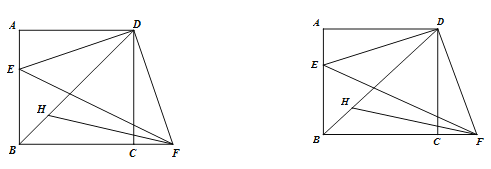
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
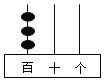
ЁОЬтФПЁПАб3ПХЫужщЗХдкМЦЪ§ЦїЕФ3ИљВхАєЩЯЙЙГЩвЛИіЪ§зжЃЌР§ШчЃЌШчЭМАкЗХЕФЫужщБэЪОЪ§300ЃЎЯжНЋ3ПХЫужщШЮвтАкЗХдкет3ИљВхАєЩЯЃЎ
ЃЈ1ЃЉШєЙЙГЩЕФЪ§ЪЧСНЮЛЪ§ЃЌдђЪЎЮЛЪ§зжЮЊ1ЕФИХТЪЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓЙЙГЩЕФЪ§ЪЧШ§ЮЛЪ§ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЪЬтЧщОГЃЉ вбжЊОиаЮЕФУцЛ§ЮЊaЃЈaЮЊГЃЪ§ЃЌaЃО0ЃЉЃЌЕБИУОиаЮЕФГЄЮЊЖрЩйЪБЃЌЫќЕФжмГЄзюаЁЃПзюаЁжЕЪЧЖрЩйЃП
ЃЈЪ§бЇФЃаЭЃЉ
ЩшИУОиаЮЕФГЄЮЊxЃЌжмГЄЮЊyЃЌдђyгыxЕФКЏЪ§ЙиЯЕЪНЮЊy=2ЃЈ![]() ЃЉЃЈxЃО0ЃЉ
ЃЉЃЈxЃО0ЃЉ
ЃЈЬНЫїбаОПЃЉ
ЮвУЧПЩвдНшМјвдЧАбаОПКЏЪ§ЕФОбщЃЌЯШЬНЫїКЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓКЭаджЪЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓКЭаджЪЃЎ
ЃЈ1ЃЉЂйЬюаДЯТБэЃЌЛГіКЏЪ§ЕФЭМЯѓЃЛ

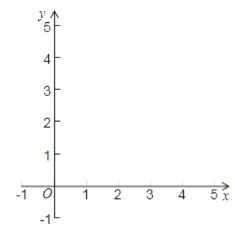
ЂкЙлВьЭМЯѓЃЌаДГіИУКЏЪ§СНЬѕВЛЭЌРраЭЕФаджЪЃЛ
ЂлдкЧѓЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФзюДѓЃЈаЁЃЉжЕЪБЃЌГ§СЫЭЈЙ§ЙлВьЭМЯѓЃЌЛЙПЩвдЭЈЙ§ХфЗНЕУЕНЃЎЧыФуЭЈЙ§ХфЗНЧѓКЏЪ§y=![]() ЃЈxЃО0ЃЉЕФзюаЁжЕЃЎ
ЃЈxЃО0ЃЉЕФзюаЁжЕЃЎ
НтОіЮЪЬтЃКЃЈ2ЃЉгУЩЯЪіЗНЗЈНтОіЁАЮЪЬтЧщОГЁБжаЕФЮЪЬтЃЌжБНгаДГіД№АИЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
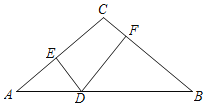
ЁОЬтФПЁПШчЭМЃЌдкЕШбќШ§НЧаЮACBжаЃЌACЃНBCЃН10ЃЌABЃН16ЃЌDЮЊЕзБпABЩЯвЛЖЏЕу(ВЛгыЕуAЃЌBжиКЯ)ЃЌDEЁЭACЃЌDFЁЭBCЃЌДЙзуЗжБ№ЮЊЕуEЃЌFЃЌдђDE+DFЕШгк_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
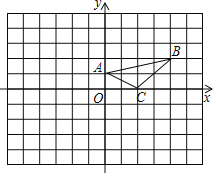
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈ0ЃЌ1ЃЉЃЌBЃЈ4ЃЌ2ЃЉЃЌCЃЈ2ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉНЋЁїABCбиyжсЗелЕУЕНЁїA1B1C1ЃЌЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉНЋЁїABCШЦзХЕуЃЈЉ1ЃЌЉ1ЃЉа§зЊ180ЁуЕУЕНЁїA2B2C2ЃЌЛГіЁїA2B2C2ЃЛ
ЃЈ3ЃЉЯпЖЮB2C2ПЩвдПДГЩЪЧЯпЖЮB1C1ШЦзХЦНУцжБНЧзјБъЯЕжаФГвЛЕуФцЪБеыа§зЊЕУЕНЃЌжБНгаДГіа§зЊжааФЕФзјБъЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. вЊСЫНтЮвЪаОгУёЕФЕЭЬМЩњЛюзДПіЃЌЪЪвЫВЩгУГщбљЕїВщЕФЗНЗЈ
B. вЛзщЪ§Он2ЃЌ2ЃЌ3ЃЌ6ЕФжкЪ§КЭжаЮЛЪ§ЖМЪЧ2
C. ЁАжРвЛУЖгВБве§УцГЏЩЯЕФИХТЪЪЧ![]() ЁБЃЌБэЪОУПХзгВБв2ДЮОЭга1ДЮе§УцГЏЩЯ
ЁБЃЌБэЪОУПХзгВБв2ДЮОЭга1ДЮе§УцГЏЩЯ
D. ЫцЛњГщШЁМзввСНУћЭЌбЇЕФ5ДЮЪ§бЇГЩМЈЃЌЦНОљЗжЖМЪЧ90ЗжЃЌЗНВюЗжБ№ЪЧSМз2ЃН5ЃЌSвв2ЃН10ЃЌЫЕУїввЕФГЩМЈНЯЮЊЮШЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕу
ЕФЭМЯѓНЛгкЕу![]() КЭ
КЭ![]() ЃЎ
ЃЎ
![]() ЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
![]() ЧыжБНгаДГі
ЧыжБНгаДГі![]() ЪБЃЌxЕФШЁжЕЗЖЮЇЃЛ
ЪБЃЌxЕФШЁжЕЗЖЮЇЃЛ
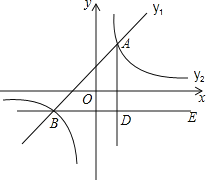
![]() Й§ЕуBзї
Й§ЕуBзї![]() жсЃЌ
жсЃЌ![]() гкЕуDЃЌЕуCЪЧжБЯпBEЩЯвЛЕуЃЌШє
гкЕуDЃЌЕуCЪЧжБЯпBEЩЯвЛЕуЃЌШє![]() ЃЌЧѓЕуCЕФзјБъЃЎ
ЃЌЧѓЕуCЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌНЋБпABШЦЕуAЫГЪБеыа§зЊ60ЁуЕУЕНЯпЖЮADЃЌНЋБпACШЦЕуAФцЪБеыа§зЊ120ЁуЕУЕНЯпЖЮAEЃЌСЌНгDE.
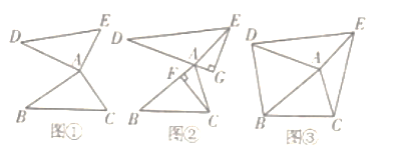
ЃЈ1ЃЉЁЂШчЭМЂйЃЌЕБЁЯBAC=90ЁуЪБЃЌШєЁїABCЕФУцЛ§ЮЊ5ЃЌдђЁїADEЕФУцЛ§ЮЊ________ЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌCFЁЂBGЗжБ№ЪЧЁїABCКЭЁїADEЕФИпЃЌШєЁїABCЮЊШЮвтШ§НЧаЮЃЌЁїABCгыЁїADEЕФУцЛ§ЪЧЗёЯрЕШЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌСЌНгBDЁЂCE.ШєAB=4ЃЌAC=2![]() ЃЌЫФБпаЮCEDBЕФУцЛ§ЮЊ13
ЃЌЫФБпаЮCEDBЕФУцЛ§ЮЊ13![]() ЃЌдђЁїABCЕФУцЛ§ЮЊ________.
ЃЌдђЁїABCЕФУцЛ§ЮЊ________.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com