练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．计算：$\sqrt{10{x}^{3}y}$•$\sqrt{40xy}$．

    分析 根据二次根式的乘法法则进行运算即可．

    解答 解：$\sqrt{10{x}^{3}y}$•$\sqrt{40xy}$
    =$\sqrt{10{x}^{3}y•40xy}$
    =$\sqrt{400{x}^{4}•{y}^{2}}$
    =20x2y．

    点评 此题主要考查二次根式的乘法，会运用乘法法则进行计算和化简是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届广东省南雄市九年级下学期模拟考试数学试卷（解析版） 题型：单选题

    方程x2－2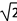x＋2＝0的根的情况为( )

    A. 有一个实数根 B. 有两个不相等的实数根 C. 没有实数根 D. 有两个相等的实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算下列各题：
    （1）（$\sqrt{2}$-2）（$\sqrt{2}$+2）
    （2）（$\sqrt{5}$+3$\sqrt{2}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

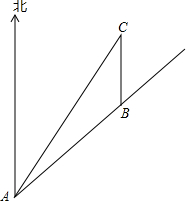    9．如图，一条笔直的公路经过两个城镇A和B，为了改善居住条件，当地要建设一个新城镇C，已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处，且位于城镇B的正北方向，已知AB=4$\sqrt{2}$km，求新城镇C到公路的距离．（结果保留到0.1km，参考数据：$\sqrt{3}$≈1.73，$\sqrt{2}$≈1.41，$\sqrt{6}$≈2.45）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

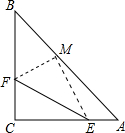    16．如图，△ABC中，CA=CB，∠ACB=90°，E、F分别在CA、CB上，将△CEF沿直线EF翻折，点C恰好落在AB上的点M处，若AM=3BM，求$\frac{CF}{CE}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．抛物线y=-x2+5x+6的顶点A（$\frac{5}{2}$，$\frac{49}{4}$），与x轴交点B（-1，0），C（6，0），△ABC的面积为$\frac{343}{8}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知点A（2，m）在直线y=-2x+8上．
    （1）点A（2，m）向左平移3个单位后的坐标是（-1，4）；直线y=-2x+8向左平移3个单位后的直线解析式是y=-2x+2；
    （2）求直线y=-2x+8绕点P（0，8）顺时针旋转90°后的直线解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

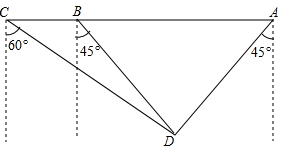    10．如图，某海监船向正西方向航行，在A处望见一艘正在作业渔船D在南偏西45°方向上，海监船航行到B处时望见渔船D在南偏东45°方向上，又航行了半小时到达C处，望见渔船D在南偏东60°方向上，若海监船的速度为40海里/时，求A，B之间的距离．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知二次函数y=x2-2015x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x的一元二次方程x2-2015x+m=0的两个实数根是x1=1，x2=2014．

    查看答案和解析>>

    同步练习册答案