
分析 (1)先求出m的值,再根据平移的性质可得出平移后的坐标;直接根据函数图象平移的性质可得出直线y=-2x+8向左平移3个单位后的直线解析式;
(2)设顺时针旋转后直线的解析式为y=$\frac{1}{2}$x+b,再把P(0,8)代入求出b的值即可.
解答 解:(1)∵点A(2,m)在直线y=-2x+8上,
∴-4+8=m,即m=4,
∴A(2,4),
∴向左平移3个单位后的坐标是(-1,4).
∵直线y=-2x+8向左平移3个单位,
∴平移后的直线解析式为y=-2(x+3)+8=-2x+2.
故答案为:(-1,4),y=-2x+2;
(2)设顺时针旋转后直线的解析式为y=$\frac{1}{2}$x+b,
∵P(0,8),
∴b=8,
∴顺时针旋转90°后的直线解析式为:y=-$\frac{1}{2}$x+8.
点评 本题考查的是一次函数的图象与几何变换,熟知函数图象平移的规律是解答此题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:判断题
如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.
(1)当运动时间t为多少秒时,PQ∥CD.
(2)当运动时间t为多少秒时,以点P,Q,E,D为顶点的四边形是平行四边形

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
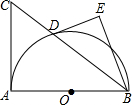 已知,如图,AB是半圆的直径,AC切半圆于A,CB交⊙O于D,DE切⊙O于D,BE⊥DE,垂足是E,BD=10,DE,BE是方程x2-2(m+2)x+2m2-m+3=0的两个根(DE<BE),求AC的长.
已知,如图,AB是半圆的直径,AC切半圆于A,CB交⊙O于D,DE切⊙O于D,BE⊥DE,垂足是E,BD=10,DE,BE是方程x2-2(m+2)x+2m2-m+3=0的两个根(DE<BE),求AC的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com