
分析 先求出每个式子的倒数,根据倒数即可比较两数的大小.
解答 解:$\frac{1}{\sqrt{6}-\sqrt{5}}$=$\frac{\sqrt{6}+\sqrt{5}}{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}$=$\frac{\sqrt{6}+\sqrt{5}}{(\sqrt{6})^{2}-(\sqrt{5})^{2}}$=$\sqrt{6}$+$\sqrt{5}$.$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}}$=$\sqrt{3}$+$\sqrt{2}$.
∵$\sqrt{6}$+$\sqrt{5}$>$\sqrt{3}$+$\sqrt{2}$>0,$\frac{1}{\sqrt{6}-\sqrt{5}}$>$\frac{1}{\sqrt{3}-\sqrt{2}}$>0,
∴$\sqrt{6}$-$\sqrt{5}$<$\sqrt{3}$-$\sqrt{2}$.
点评 本题考查了二次根式的性质,分母有理化,实数的大小比较等知识点,主要考查学生能否选择适当的方法比较两实数的大小,题目比较好.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
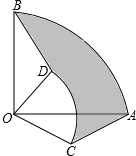 把两个圆心角都是90°的扇形OAB与扇形OCD按如图所示位置叠放在一起,连接AC,BD.
把两个圆心角都是90°的扇形OAB与扇形OCD按如图所示位置叠放在一起,连接AC,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
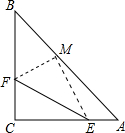 如图,△ABC中,CA=CB,∠ACB=90°,E、F分别在CA、CB上,将△CEF沿直线EF翻折,点C恰好落在AB上的点M处,若AM=3BM,求$\frac{CF}{CE}$.
如图,△ABC中,CA=CB,∠ACB=90°,E、F分别在CA、CB上,将△CEF沿直线EF翻折,点C恰好落在AB上的点M处,若AM=3BM,求$\frac{CF}{CE}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{9}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com