
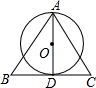
 已知:如图.AD是⊙O的直径,直线BC经过点D,并且AB=AC,∠BAD=∠CAD.求证:直线BC是⊙O的切线.
已知:如图.AD是⊙O的直径,直线BC经过点D,并且AB=AC,∠BAD=∠CAD.求证:直线BC是⊙O的切线.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:判断题
已知某二次函数的图象与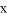 轴分别相交于点
轴分别相交于点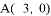 和点
和点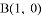 ,与
,与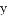 轴相交于
轴相交于 ,顶点为点
,顶点为点 。
。
⑴求该二次函数的解析式(系数用含 的代数式表示);
的代数式表示);
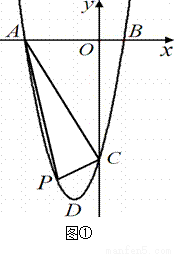
⑵如图①,当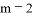 时,点
时,点 为第三象限内抛物线上的一个动点,设
为第三象限内抛物线上的一个动点,设 的面积为
的面积为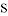 ,试求出
,试求出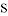 与点
与点 的横坐标
的横坐标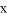 之间的函数关系式及
之间的函数关系式及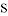 的最大值;
的最大值;
⑶如图②,当 取何值时,以
取何值时,以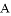 、
、 、
、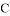 三点为顶点的三角形与
三点为顶点的三角形与 相似?
相似?

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
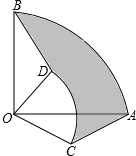 把两个圆心角都是90°的扇形OAB与扇形OCD按如图所示位置叠放在一起,连接AC,BD.
把两个圆心角都是90°的扇形OAB与扇形OCD按如图所示位置叠放在一起,连接AC,BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
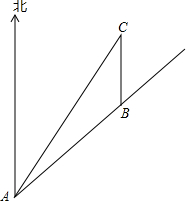 如图,一条笔直的公路经过两个城镇A和B,为了改善居住条件,当地要建设一个新城镇C,已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处,且位于城镇B的正北方向,已知AB=4$\sqrt{2}$km,求新城镇C到公路的距离.(结果保留到0.1km,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)
如图,一条笔直的公路经过两个城镇A和B,为了改善居住条件,当地要建设一个新城镇C,已知新城镇C在城镇A的北偏东30°方向距城镇A 8km处,且位于城镇B的正北方向,已知AB=4$\sqrt{2}$km,求新城镇C到公路的距离.(结果保留到0.1km,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,$\sqrt{6}$≈2.45)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
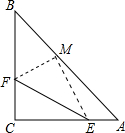 如图,△ABC中,CA=CB,∠ACB=90°,E、F分别在CA、CB上,将△CEF沿直线EF翻折,点C恰好落在AB上的点M处,若AM=3BM,求$\frac{CF}{CE}$.
如图,△ABC中,CA=CB,∠ACB=90°,E、F分别在CA、CB上,将△CEF沿直线EF翻折,点C恰好落在AB上的点M处,若AM=3BM,求$\frac{CF}{CE}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
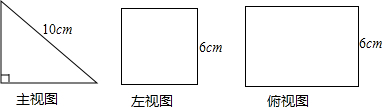
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com