
分析 先把原式变形为$\frac{\sqrt{3}-1}{\sqrt{3}(\sqrt{2}-1)-\sqrt{2}(\sqrt{2}-1)}$=$\frac{\sqrt{3}-1}{(\sqrt{3}-\sqrt{2})(\sqrt{2}-1)}$,再分母有理化即可求解.
解答 解:$\frac{\sqrt{3}-1}{\sqrt{6}+\sqrt{2}-2-\sqrt{3}}$
=$\frac{\sqrt{3}-1}{\sqrt{3}(\sqrt{2}-1)-\sqrt{2}(\sqrt{2}-1)}$
=$\frac{\sqrt{3}-1}{(\sqrt{3}-\sqrt{2})(\sqrt{2}-1)}$
=($\sqrt{3}$-1)($\sqrt{3}$+$\sqrt{2}$)($\sqrt{2}$+1)
=$\sqrt{3}$+2$\sqrt{2}$+1
点评 本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
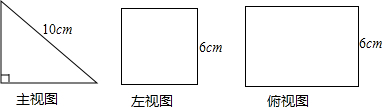
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
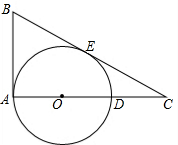 如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.
如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲、乙都正确 | B. | 甲正确,乙不正确 | C. | 甲、乙都不正确 | D. | 乙正确,甲不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
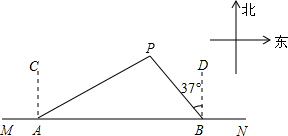 如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).
如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com