【题目】如图，一段抛物线：y=﹣x（x﹣3）（0≤x≤3），记为C1，它与x轴交于点O，A1；
将C1绕点A1旋转180°得C2，交x轴于点A2；
将C2绕点A2旋转180°得C3，交x轴于点A3；
…
如此进行下去，直至得C13．若P（37，m）在第13段抛物线C13上，则m=_____．
超能学典应用题题卡系列答案科目：初中数学 来源： 题型：
【题目】如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连ME．
正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE．
（下面请你完成余下的证明过程）
（2）若将(1)中的“正方形ABCD”改为“正三角形ABC”（如图2）,N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
（3）若将（1）中的“正方形ABCD”改为“正
边形ABCD…X”，请你作出猜想：当∠AMN=°时，结论AM=MN仍然成立．（直接写出答案，不需要证明）
图1 图2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果反比例函数的图象经过点（3，﹣5），那么这个反比例函数的图象一定经过点（ ）
A. （3，5） B. （﹣3，5） C. （﹣3，﹣5） D. （0，﹣5）
查看答案和解析>>
科目：初中数学 来源： 题型：
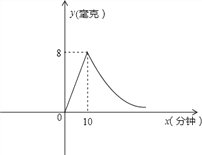
【题目】为预防甲型H1N1流感，某校对教室喷洒药物进行消毒．已知喷洒药物时每立方米空气中的含药量y（毫克）与时间x（分钟）成正比，药物喷洒完后，y与x成反比例（如图所示）．现测得10分钟喷洒完后，空气中每立方米的含药量为8毫克．
（1）求喷洒药物时和喷洒完后，y关于x的函数关系式；
（2）若空气中每立方米的含药量低于2毫克学生方可进教室，问消毒开始后至少要经过多少分钟，学生才能回到教室？
（3）如果空气中每立方米的含药量不低于4毫克，且持续时间不低于10分钟时，才能杀灭流感病毒，那么此次消毒是否有效？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（满分6分）如图，在平面直角坐标系中，已知点B(4，2)，BA⊥
轴于A．
(1)画出将△OAB绕原点旋转180°后所得的△OA1B1 ，并写出点B1 的坐标；
(2)将△OAB平移得到△O2A2B2，点A的对应点是A2（2，-4），点B的对应点B2
在坐标系中画出△O2A2B2 ；并写出B2的坐标；
(3)△OA1B1与△O2A2B2成中心对称吗？若是， 请直接写出对称中心点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）发现：如图1，点A为线段BC外一动点，且BC=a，AB=b．
①填空：当点A位于 时，线段AC的长取得最大值，且最大值为 （用含a，b的式子表示）
（2）应用：点A为线段BC外一动点，且BC=3，AB=1，如图2所示，分别以AB、AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．
①请找出图中与BE相等的线段，并说明理由；
②直接写出线段BE长的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
