
����Ŀ����1�����֣���ͼ1����AΪ�߶�BC��һ���㣬��BC=a��AB=b��
����գ�����Aλ���� ��ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ�� �����ú�a��b��ʽ�ӱ�ʾ��
��2��Ӧ�ã���AΪ�߶�BC��һ���㣬��BC=3��AB=1����ͼ2��ʾ���ֱ���AB��ACΪ�ߣ����ȱ�������ABD�͵ȱ�������ACE������CD��BE��
�����ҳ�ͼ����BE��ȵ��߶Σ���˵�����ɣ�
��ֱ��д���߶�BE�������ֵ��

���𰸡���1��CB���ӳ����ϣ�a+b����2����CD=BE�����ɼ����������߶�BE�������ֵΪ4�����ɼ�����.
�������������������1�����ݵ�AΪ�߶�BC��һ���㣬��BC=a��AB=b���ɵõ���Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪBC+AB=a+b��
��2���ٸ��ݵȱ�������ABD�͵ȱ�������ACE���ɵ���CAD�ա�EAB��SAS��������ȫ�������ε����ʿɵ�CD=BE��
�ڸ���ȫ�������ε����ʿɵã��߶�BE�������ֵ=�߶�CD�������ֵ�������߶�CD�ij�ȡ�����ֵʱ����D��CB���ӳ����ϣ���ʱCD=3+1=4���ɵ�BE=4��
�����������1����ͼ1��

�ߵ�AΪ�߶�BC��һ���㣬��BC=a��AB=b��
�൱��Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪBC+AB=a+b��
��2����CD=BE��
���ɣ���ͼ2��
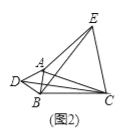
��������ABD��������ACE�ǵȱ���������
��AD=AB��AC=AE����BAD=��CAE=60����
���BAD+��BAC=��CAE+��BAC��
����CAD=��EAB��
����CAD����EAB��

���CAD�ա�EAB��SAS����
��CD=BE��
���߶�BE�������ֵΪ4��
���ɣ����߶�BE�������ֵ=�߶�CD�������ֵ��
�൱�߶�CD�ij�ȡ�����ֵʱ����D��CB���ӳ����ϣ�
��ʱCD=3+1=4��
��BE=4��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������ߣ�y=��x��x��3����0��x��3������ΪC1������x�ύ�ڵ�O��A1��
��C1�Ƶ�A1��ת180����C2����x���ڵ�A2��
��C2�Ƶ�A2��ת180����C3����x���ڵ�A3��
��
��˽�����ȥ��ֱ����C13����P��37��m���ڵ�13��������C13�ϣ���m=_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й�����ĸ���������š���������ˮ��Ϊ67500�֣�����67500�ÿ�ѧ��������ʾΪ��������
A.0.675��105
B.6.75��104
C.67.5��103
D.675��102
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��E��AB���е㣬����DE���ӳ���CB���ӳ����ڵ�F����M��BC���ϣ��ҡ�MDF=��ADF��
��1����֤����ADE�ա�BFE��
��2������EM�����FM=DM���ж�EM��DF�Ĺ�ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b��10�� ab��11�������ʽa2��ab��b2��ֵ�ǣ� ��
A.��67B.67C.��89D.89
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�ԭ����������Ϊ8Ԫ����Ʒ��10Ԫ�۳���ÿ�������200��.���ڲ�������ۼۣ����ٽ������ķ���������������֪ÿ����Ʒ�Ǽ�1Ԫ��ÿ����������ͼ���20��.��������Ʒÿ���Ǽ�![]() Ԫ��
Ԫ��
��1����գ�ԭ��ÿ����Ʒ�������� Ԫ���Ǽۺ�ÿ����Ʒ��ʵ�������� Ԫ �����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2��Ϊ��ʹÿ����700Ԫ�������ۼ�Ӧ��Ϊ����Ԫ��
(3)�ۼ۶�Ϊ����Ԫʱ��ÿ�����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���������֣��������.
���֪��![]() ������������������������ѭ��С�������
������������������������ѭ��С�������![]() ��С���������Dz�����ȫ����д��������������1��
��С���������Dz�����ȫ����д��������������1��![]() ��2������
��2������![]() ����������Ϊ1����
����������Ϊ1����![]() ��ȥ����������1�������С������
��ȥ����������1�������С������![]() -1���������ϵ����ݣ������������⣺
-1���������ϵ����ݣ������������⣺
��1��![]() ������������ ���������� ��
������������ ���������� ��
��2��1+![]() ������������ ���������� ��
������������ ���������� ��
��3������2+![]() ����������x��С��������y����x-y��ֵ��
����������x��С��������y����x-y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ѳ�����ֽƬABCD��EF�۵���ʹ�õ�D���B�غϣ���C���ڵ�C���λ���ϣ�

��1���۵���DC�Ķ�Ӧ�߶��� ��CF�Ķ�Ӧ�߶��� ��
��2����EBF�ǵ�������������˵�����ɣ�
��3����AB=4��AD=8������EBF�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com