
【题目】某商店原来将进货价为8元的商品按10元售出,每天可销售200件.现在采用提高售价,减少进货量的方法来增加利润,已知每件商品涨价1元,每天的销售量就减少20件.设这种商品每个涨价![]() 元.
元.
(1)填空:原来每件商品的利润是 元,涨价后每件商品的实际利润是 元 (可用含![]() 的代数式表示);
的代数式表示);
(2)为了使每天获得700元的利润,售价应定为多少元?
(3)售价定为多少元时,每天利润最大,最大利润是多少元?
【答案】(1) 2;2+ ![]() ;(2)售价应定为13元或15元;(3)当涨价4元(即售价为14元)时,每天利润最大,最大利润为720元.
;(2)售价应定为13元或15元;(3)当涨价4元(即售价为14元)时,每天利润最大,最大利润为720元.
【解析】试题分析:(1)根据利润=售价-进价表示出商品的利润即可;
(2)设应将售价提为x元时,才能使得所赚的利润最大为y元,根据题意可得:y=(10+x-8)(200-2x),令y=700,解出x的值即可;
(3)根据总利润w=单件利润×销售量列出函数表达式,运用二次函数性质解答即可.
试题解析:(1)原来每件商品的利润是2元;涨价后每件商品的实际利润是2+x元;
故答案为:2,(2+x);
(2)根据题意,得(2+x)(200-20x)=700.
整理,得x2-8x+15=0,
解这个方程得x1=3x2=5,
所以10+3=13,10+5=15.
答:售价应定为13元或15元;
(3)设利润为w,由题意得,每天利润为w=(2+x)(200-x).
w=(2+x)(200-x)=-20x2+160x+400,
=-20(x-4)2+720.
所以当涨价4元(即售价为14元)时,每天利润最大,最大利润为720元.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】(满分6分)如图,在平面直角坐标系中,已知点B(4,2),BA⊥![]() 轴于A.
轴于A.
(1)画出将△OAB绕原点旋转180°后所得的△OA1B1 ,并写出点B1 的坐标;
(2)将△OAB平移得到△O2A2B2,点A的对应点是A2(2,-4),点B的对应点B2
在坐标系中画出△O2A2B2 ;并写出B2的坐标;
(3)△OA1B1与△O2A2B2成中心对称吗?若是, 请直接写出对称中心点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
①填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB、AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
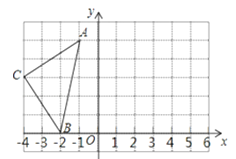
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣2,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A'B′C′(其中A'、B′、C′分别是A、B、C的对称点,不写画法);
(2)写出C′的坐标,并求△ABC的面积;
(3)在y轴上找出点P的位置,使线段PA+PB的最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是一元二次方程2x2-2x+m+1=0的两个实根.
(1)求实数m的取值范围;
(2)如果m满足不等式7+4x1x2>x12+x22,且m为整数.求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com