
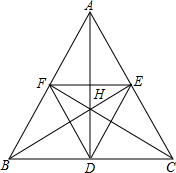
 如图,锐角△ABC的垂心为H,三条高的垂足分为D、E、F,则H是△DEF的( )
如图,锐角△ABC的垂心为H,三条高的垂足分为D、E、F,则H是△DEF的( )| A. | 垂心 | B. | 重心 | C. | 内心 | D. | 外心 |
分析 根据垂心的定义可得四点共圆:BE丄AC,CF丄AB,四点B、C、E、F共圆,HD丄BD,HF丄BF,则四点C、D、H、E共圆,进一步利用圆周角定理得出:∠EBF=∠FCE,∠HBF=∠FDH,∠HDE=∠HCE,证得DA平分∠EDF即可.
解答 解:∵BE丄AC,CF丄AB,
∴四点B、C、E、F共圆(以BC为直径),
∴∠EBF=∠FCE,
∵HD丄BD,HF丄BF,
∴四点B、D、H、F共圆(以BH为直径),
∴∠HBF=∠FDH,
同理,四点C、D、H、E共圆,(以CH为直径),∠HDE=∠HCE,
∴∠HDE=∠HDF,
∴DA平分∠EDF即可.
同理可证EB平分∠DEF,FC平分∠EFD,
∴H是△DEF的角平分线的交点,
∴H是△DEF的内心.
故选:C.
点评 此题考查三角形的五心,掌握四点共圆以及圆周角定理是解决问题的关键.


科目:初中数学 来源: 题型:解答题
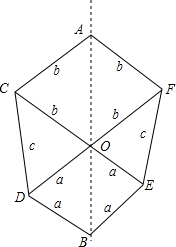 (1)制作如图①的纸片,并沿对称轴AB把它剪开;
(1)制作如图①的纸片,并沿对称轴AB把它剪开;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
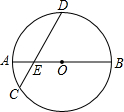 如图,⊙O的直径AB和弦CD相交于点E,∠DEB=45°.
如图,⊙O的直径AB和弦CD相交于点E,∠DEB=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com