
【题目】(1)如图,已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.

(2)如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?

【答案】(1)AB=10,CD=4.8;(2)BM=30厘米.
【解析】
(1)在直角三角形ABC中,利用勾股定理求出AB的长,再利用面积法求出CD的长即可.
(2)连接AC,BD交于点O,根据四边形ABCD是菱形求出AO的长,然后根据勾股定理求出BO的长,于是可以求出B、M两点的距离.
解:(1)在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,
由勾股定理得:AB= ![]() =10,
=10,
∵S△ABC= ![]() ABCD=
ABCD= ![]() ACBC,∴CD=
ACBC,∴CD= ![]() =
=![]() =4.8
=4.8
(2).连接AC,BD交于点O,
∵四边形ABCD是菱形,
∴AO= ![]() AC=12厘米,AC⊥BD,
AC=12厘米,AC⊥BD,
∴BO= ![]() =
= ![]() =5厘米,
=5厘米,
∴BD=2BO=10厘米,
∴BM=3BD=30厘米.
故答案为:(1)AB=10,CD=4.8;(2)BM=30厘米.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
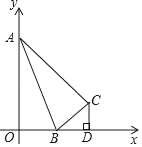
【题目】如图,长度为5的动线段![]() 分别与坐标系横轴、纵轴的正半轴交于点
分别与坐标系横轴、纵轴的正半轴交于点![]() 、点
、点![]() ,点
,点![]() 和点
和点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,过点
,过点![]() 作
作![]() 轴的垂线段
轴的垂线段![]() ,交
,交![]() 轴于点
轴于点![]()
(1)移动点![]() ,发现在某一时刻,
,发现在某一时刻,![]() 和以点
和以点![]() 为顶点的三角形相似,求这一时刻点
为顶点的三角形相似,求这一时刻点![]() 的坐标;
的坐标;
(2)移动点![]() ,当
,当![]() 时求点
时求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形![]() 和
和![]() 分别是边长为
分别是边长为![]() 和
和![]() 的正方形.
的正方形.

(1)用含![]() 和
和![]() 的代数式表示图中三角形
的代数式表示图中三角形![]() 的面积.
的面积.
(2)用用![]() 和
和![]() 的代数式表示图中阴影部分的面积.
的代数式表示图中阴影部分的面积.
(3)小军计算出当![]() ,
,![]() 时的阴影部分面积,与小明计算的当
时的阴影部分面积,与小明计算的当![]() ,
,![]() 时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积.
时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2![]() 的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ;连接PQ,PQ与BC交于点E,QP延长线与AD(或AD延长线)交于点F,连接CQ.求证:
的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ;连接PQ,PQ与BC交于点E,QP延长线与AD(或AD延长线)交于点F,连接CQ.求证:
(1)CQ=AP;
(2)△APB∽△CEP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.

已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出了不同的优惠方案:在甲超市累计购买商品超出300元后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元后,超出部分按原价8.5折优惠.若顾客累计购买商品工(x> 300)元.
(1)请用含x的式子分别表示顾客在两家超市购物应付的费用;
(2)若x= 500时,选择哪家超市购物更优惠?说明理由;
(3)若x=1 000时,选择哪家超市购物更优惠?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com