
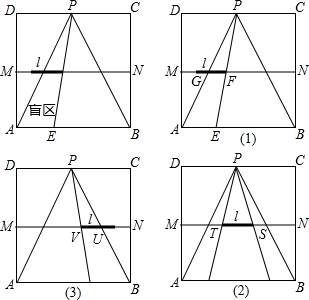
分析 (1)根据题意涂上阴影即可;
(2)根据正方形的性质得AM=2,盲区为梯形,且上底为下底的一半,高为2,然后分段计算:梯形的上底、下底,然后根据梯形的面积分别计算出三中情况下的梯形的面积即可;根据一次函数的性质求解.
解答 解 (1)如图: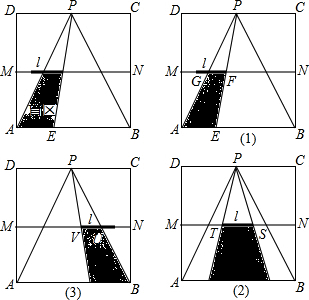 .
.
(2)①当1≤t≤2时,△PAB内的盲区是梯形AEFG.
FG是△PAE的中位线,FG=t-1,AE=2(t-1).而梯形AEFG的高为2,
∴y=$\frac{1}{2}$[(t-1)+2(t-1)]×2=3t-3.
②当2≤t≤3时,△PAB内的盲区是梯形QRST.
易知TS=1,QR=2,而梯形QRST的高为2,
∴y=$\frac{1}{2}$(1+2)×2=3.
③当3≤t≤4时,△PAB内的盲区是梯形WBUV.
易知UV=1-(t-3)=4-t,WB=2(4-t),而梯形的高为2,∴y=$\frac{1}{2}$[(4-t)+2(4-t)]×2=12-3t.
当1≤t≤2时,盲区的面积由0逐渐增大到3;
当2≤t≤3时,盲区的面积y为定值3;
当3≤t≤4时,盲区的面积由3逐渐减小到0.
点评 本题考查了视点、视角和盲区:把观察者所处的位置定为一点,叫视点.人眼到视平面的距离视固定的(视距),视平面左右两个边缘到人眼的连线得到的角度就是视角.视线到达不了的区域为盲区


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
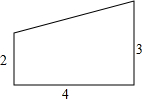 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com