
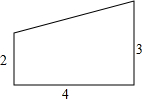
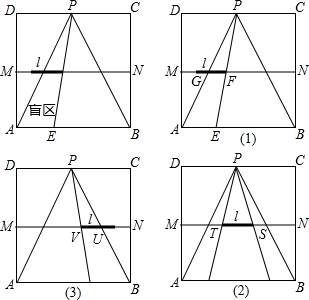
 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5. 分析 根据题意,分两种情况讨论,求出每种情况下直角三角形的斜边的长度各是多少;然后用斜边的长度除以2,求出直角三角形的外接圆的半径是多少,即可求出能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是多少.
解答 解:(1)如图1,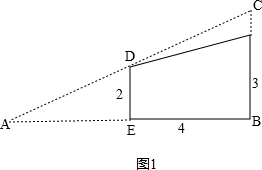 ,
,
当D、E分别是斜边AC、直角边AB的中点时,
∵D、E分别是斜边AC、直角边AB的中点,
∴$\frac{AE}{AB}=\frac{DE}{BC}=\frac{1}{2}$,
∴BC=2×2=4,AE=BE=4,AB=4+4=8,
∴AC=$\sqrt{{4}^{2}{+8}^{2}}=4\sqrt{5}$,
∴直角三角形ABC的外接圆的半径是:
4$\sqrt{5}÷2=2\sqrt{5}$,
即能刚好完全覆盖原直角三角形纸片的圆形纸片的半径是2$\sqrt{5}$.
(2)如图2,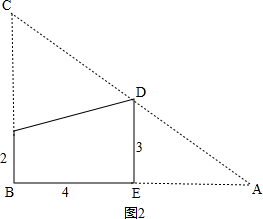 ,
,
当D、E分别是斜边AC、直角边AB的中点时,
∵D、E分别是斜边AC、直角边AB的中点,
∴$\frac{AE}{AB}=\frac{DE}{BC}=\frac{1}{2}$,
∴BC=3×2=6,AE=BE=4,AB=4+4=8,
∴AC=$\sqrt{{6}^{2}{+8}^{2}}=10$,
∴直角三角形ABC的外接圆的半径是:
10÷2=5,
即能刚好完全覆盖原直角三角形纸片的圆形纸片的半径是5.
综上,可得
能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
故答案为:2$\sqrt{5}$或5.
点评 (1)此题主要考查了图形的剪拼问题,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是求出原来直角三角形纸片的斜边的长度是多少.
(2)此题还考查了直角三角形的外接圆的半径的求法,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
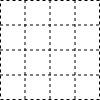 在下面的正方形网格中,每个小正方形的边长都是1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个三角形,使三边长分别为3,$\sqrt{10}$,5,并求此三角形的面积.
在下面的正方形网格中,每个小正方形的边长都是1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个三角形,使三边长分别为3,$\sqrt{10}$,5,并求此三角形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 种植户 | 豌豆 | 土豆 | 卖出两种农产品总收入(万元) | ||
| 种植面积(亩) | 每亩产量(吨) | 种植面积(亩) | 每亩产量(吨) | ||
| 甲 | 4 | 1 | 4 | 3 | 4.8 |
| 乙 | 8 | 1 | 2 | 2.5 | 5.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com