
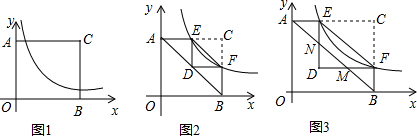
分析 (1)把E的横坐标代入y=$\frac{3}{x}$中即可得到结果;
(2)根据△ECF沿直线EF翻折180°,点C恰好落在线段AB上的D点处,得到CE=DE=AE,CF=DF=BF,求得D($\frac{1}{2}$t,$\frac{1}{2}$t),E($\frac{1}{2}$t,t),由于点E在函数y=$\frac{3}{x}$的图象上,代入反比例函数的解析式即可得到结果;
(3)设OA=OB=t,由于点F在反比例函数y=$\frac{3}{x}$的图象上,得到F(t,$\frac{3}{t}$),E($\frac{3}{t}$,t),根据△ECF沿直线EF翻折180°得到△EDF,求得D($\frac{3}{t}$,$\frac{3}{t}$),得到△BFM是等腰直角三角形,根据题意列方程即可得到结论.
解答 解:(1)∵y=$\frac{3}{x}$的图象与AC交于点E,点E的横坐标为1,
∴y=$\frac{3}{1}$=3,
∴E(1,3),
∴OA=OB=3,
∴t=3;
(2)∵△ECF沿直线EF翻折180°,点C恰好落在线段AB上的D点处,
∴CE=DE=AE,CF=DF=BF,
∴D($\frac{1}{2}$t,$\frac{1}{2}$t),E($\frac{1}{2}$t,t),∵点E在函数y=$\frac{3}{x}$的图象上,
∴$\frac{1}{2}$t•t=3,
解得:t=$\sqrt{6}$;
(3)设OA=OB=t,
∴B(t,0),A(0,t)
∵点F在反比例函数y=$\frac{3}{x}$的图象上,
∴F(t,$\frac{3}{t}$),E($\frac{3}{t}$,t),
∵△ECF沿直线EF翻折180°得到△EDF,
∴CF=DF=DE=CE,
∴D($\frac{3}{t}$,$\frac{3}{t}$),
∵四边形OABC是正方形,
∴∠OBA=∠ABF=45°,
∴△BFM是等腰直角三角形,
∴MF=BF=$\frac{3}{t}$,
∴M(t-$\frac{3}{t}$,$\frac{3}{t}$),
∴DM=DN=t-$\frac{3}{t}$-$\frac{3}{t}$=t-$\frac{6}{t}$,
当四边形NMFE的面积等于3时,
∴S△DEF-S△DMN=3,
即$\frac{1}{2}$(t-$\frac{3}{t}$)2-$\frac{1}{2}$(t-$\frac{6}{t}$)2=3,
∵此方程无解,
∴不存在这样的t值,使得四边形NMFE的面积等于3.
点评 本题考查了反比例函数的性质,反比例函数图象上点的坐标特征,正方形的性质,等腰直角三角形的性质,图形的变换-翻折,熟练掌握翻折的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
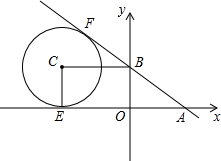 如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.
如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
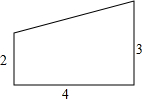 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象经过(1,2) | B. | 当x>0时,y随着x的增大而减小 | ||
| C. | 图象位于一、三象限 | D. | 该函数图象是中心对称图形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com