
分析 (1)①小明的判断正确;先求得四边形BCEG是平行四边形,进而根据AAS证得△ADF≌△EGF,即可证得FA=FG.
②小颖的判断正确;先证得AE=AC=$\frac{AB}{{\sqrt{3}}}=\frac{2AG}{{\sqrt{3}}}=GD$.然后证得△EAF≌△DGF,即可证得FA=FG.
(2)作EG⊥AC交AB于点G,连结DG,则有EG垂直平分AC,通过证得DG⊥AB,然后根据AD⊥AC,AE⊥AB即可证得四边形ADGE是平行四边形,证得GF=AF,从而证得FB=3FA.
(3)根据AD⊥AC,AE⊥AB,证得∠DAB=∠EAC,进而根据等腰三角形的性质证得∠DAB=∠DBA=∠EAC=∠ECA,得出△ACE∽△ABD,继而证得$\frac{AC}{AB}=\frac{AE}{AD}$,即可证得cos∠BAC=$\frac{AC}{AB}=\frac{AE}{AD}$,在Rt△ADG中,AD2-GD2=AD2=${(\frac{1}{2}AB)^2}$,由(1)可知:GD=AE,即可证得AD2一AE2=$\frac{1}{4}A{B^2}$.
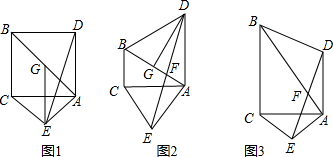
解答 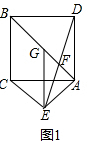 解:(1)①小明的判断正确;如图1,
解:(1)①小明的判断正确;如图1,
理由:∵在等腰三角形ABD中,∠ACB=90°,∠BAC=45°,
∴∠ABC=45°,
∵AD⊥AC,
∴AD∥BC,
∴∠DAE=45°,
∵三角形ABD是以AB为底边的等腰三角形,
∴∠ABD=45°,∠ADB=90°,
∴四边形ADBC是正方形,
∴BC=AD,
∵AE⊥AB,∠BAC=45°,
∴∠EAC=45°,
∵三角形ACE是以AC为底边等腰三角形,
∴∠ACE=45°,
∴∠ACE=∠BAC=45°,
∴AB∥CE,
∵EG⊥AC,∠ACB=90°,
∴BC∥GE,
∴四边形BCEG是平行四边形,
∴GE=BC=AD,GE∥AD,
∴∠DAF=∠GEF,
在△ADF和△EGF中,
$\left\{\begin{array}{l}{∠DAF=∠GEF}\\{∠AFD=∠GFE}\\{AD=EG}\end{array}\right.$,
∴△ADF≌△EGF(AAS),
∴FA=FG.
②小颖的判断正确,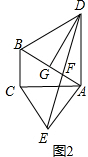 如图2,
如图2,
∵∠BAC=30°,AE⊥AB,
∴∠CAE=60°,
∵△ACE是等腰三角形,
∴△ACE是等边三角形.
同理:△ABD是等边三角形,
∴AE=AC=$\frac{AB}{{\sqrt{3}}}=\frac{2AG}{{\sqrt{3}}}=GD$.
∵DG∥AE,
∴∠AEF=∠GDF,
在△EAF和△DGF中,
$\left\{\begin{array}{l}{∠AEF=∠GDF}\\{∠AFE=∠GFD}\\{AE=GD}\end{array}\right.$,
∴△EAF≌△DGF(AAS),
∴FA=FG.
(2)作EG⊥AC交AB于点G,连结DG,则有EG垂直平分AC,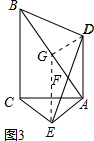 如图3,
如图3,
∵∠ACB=90°,
∴EG∥BC.
∴AG=BG.
∵AD=BD,
∴DG⊥AB,
又∵AD⊥AC,AE⊥AB,
∴EG∥AD,DG∥AE,
∴四边形ADGE是平行四边形.
∴GF=AF,
∴FB=3FA.
(3)①∵AD⊥AC,AE⊥AB,
∴∠DAB=∠EAC,
∵三角形ABD和三角形ACE是分别以AB,AC为底边的等腰三角形,
∴∠DAB=∠DBA=∠EAC=∠ECA,
∴△ACE∽△ABD.
∴$\frac{AC}{AB}=\frac{AE}{AD}$,
∴cos∠BAC=$\frac{AC}{AB}=\frac{AE}{AD}$,
②在Rt△ADG中,AD2-GD2=AD2=${(\frac{1}{2}AB)^2}$,
由(1)可知:GD=AE,
∴AD2-AE2=$\frac{1}{4}A{B^2}$.
点评 本题考查了等腰三角形的性质,平行四边形的判定和性质,三角形全等的判定和性质,等边三角形的判定和性质,三角形相似的判定和性质,熟练掌握性质定理是解题的关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
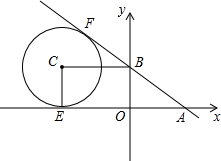 如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.
如图,在平面直角坐标系xOy中,直线y=$-\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
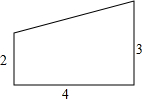 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com