
 已知抛物线C1:y=-x2-2ax-2x-a2-3a+1的顶点在直线l上,
已知抛物线C1:y=-x2-2ax-2x-a2-3a+1的顶点在直线l上,分析 (1)可用配方法将抛物线的解析式配成顶点式,设顶点坐标为(x,y),从而可用a的代数式表示x、y,消去a,就可得到x与y的关系,从而解决问题;
(2)设抛物线与直线l的交点分别为E(x1,x1+3),F(x2,x2+3),如图1,将直线l与抛物线联立,消去y,求出x,就可得到两交点的横坐标,进而得到两交点横坐标及纵坐标的差,然后运用两点之间的距离公式就可解决问题;
(3)设PQ与y轴交于点M,交x轴交于点N,如图2,易求出A、C两点的坐标,从而可求得AC=2$\sqrt{3}$,∠CAO=60°,进而可求得∠ACO=30°,∠AHQ=60°,∠ANH=60°,设ON=n,则有OM=$\sqrt{3}$n,从而可求得直线PQ的解析式为y=-$\sqrt{3}$x+$\sqrt{3}$n.设点P、Q的横坐标分别为p、q,则点P、Q的纵坐标分别为-$\sqrt{3}$p+$\sqrt{3}$n、-$\sqrt{3}$q+$\sqrt{3}$n.联立$\left\{\begin{array}{l}{y=-\sqrt{3}x+\sqrt{3}n}\\{y=-{x}^{2}+3}\end{array}\right.$,消去y,得x2-$\sqrt{3}$x+$\sqrt{3}$n-3=0①,根据根与系数的关系可得p+q=$\sqrt{3}$,pq=$\sqrt{3}$n-3,然后运用两点之间的距离公式可求出n,然后求出方程①的解,即可得到p、q,就可求出点P、点Q的坐标.
解答 解:(1)y=-x2-2ax-2x-a2-3a+1=-(x+a+1)2+2-a,
∴抛物线的顶点坐标为(-a-1,2-a),
设抛物线的顶点坐标为(x,y),
则有x=-a-1,y=2-a,
∴y-x=(2-a)-(-a-1)=3,
∴y=x+3,
∴直线l的解析式为y=x+3;
(2)证明:设抛物线与直线l的交点分别为E(x1,x1+3),F(x2,x2+3),如图1,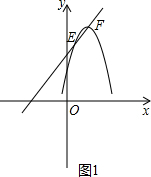
联立$\left\{\begin{array}{l}{y=x+3}\\{y=-{x}^{2}-2ax-2x-{a}^{2}-3a+1}\end{array}\right.$,
消去y得:x2+(2a+3)x+a2+3a+2=0,
∴(x+a+1)(x+a+2)=0,
∴x1=-a-1,x2=-a-2,
∴x1-x2=1,
根据两点之间距离公式可得:
EF=$\sqrt{({x}_{1}-{x}_{2})^{2}+({x}_{1}+3-{x}_{2}-3)^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴不论a为何值,抛物线与直线l的交点间的距离恒为定值;
(3)设PQ与y轴交于点M,交x轴交于点N,如图2,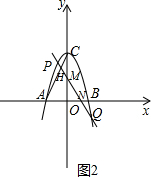
∵C1顶点C在y轴上,
∴-a-1=0,即a=-1,
∴抛物线的解析式为y=-x2+3,
∴顶点C的坐标为(0,3),OC=3.
由y=0可得0=-x2+3,
解得x1=-$\sqrt{3}$,x2=$\sqrt{3}$,
∴A(-$\sqrt{3}$,0),B($\sqrt{3}$,0),
∴OA=$\sqrt{3}$,
∴AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=2$\sqrt{3}$.
在Rt△AOC中,tan∠CAO=$\frac{OC}{OA}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴∠CAO=60°,
∴∠ACO=90°-60°=30°,
∴∠AHQ=2∠ACO=60°,
∴∠ANH=180°-∠CAO-∠AHQ=60°.
设ON=n,则OM=ON•tanONM=n•tan60°=$\sqrt{3}$n,
∴M(0,$\sqrt{3}$n),M(n,0).
可设直线PQ的解析式为y=kx+$\sqrt{3}$n,(n≠0)
则有0=kn+$\sqrt{3}$n,
解得k=-$\sqrt{3}$,
∴直线PQ的解析式为y=-$\sqrt{3}$x+$\sqrt{3}$n.
设点P、Q的横坐标分别为p、q,
则点P、Q的纵坐标分别为-$\sqrt{3}$p+$\sqrt{3}$n、-$\sqrt{3}$q+$\sqrt{3}$n.
联立$\left\{\begin{array}{l}{y=-\sqrt{3}x+\sqrt{3}n}\\{y=-{x}^{2}+3}\end{array}\right.$,
消去y,得-x2+3=-$\sqrt{3}$x+$\sqrt{3}$n,
整理得x2-$\sqrt{3}$x+$\sqrt{3}$n-3=0①,
∴p+q=$\sqrt{3}$,pq=$\sqrt{3}$n-3.
∵PQ=2AC=2×2$\sqrt{3}$=4$\sqrt{3}$,
∴PQ2=(p-q)2+(-$\sqrt{3}$p+$\sqrt{3}$n+$\sqrt{3}$q-$\sqrt{3}$n)2=48,
∴(p-q)2=(p+q)2-4pq=3-($\sqrt{3}$n-3)=12,
解得n=$\frac{\sqrt{3}}{4}$,
此时方程①为x2-$\sqrt{3}$x-$\frac{9}{4}$=0,
解得p=-$\frac{\sqrt{3}}{2}$,q=$\frac{3\sqrt{3}}{2}$.
∴点P的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{9}{4}$),点Q的坐标为($\frac{3\sqrt{3}}{2}$,-$\frac{15}{4}$).
点评 本题主要考查了用配方法求抛物线的顶点、抛物线与x轴的交点、两点之间的距离公式、特殊角的三角函数值、解一元二次方程、根与系数的关系、完全平方公式、抛物线与直线的交点坐标等知识,对运算能力的要求比较高,将两点之间的距离公式与根与系数的关系相结合,是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
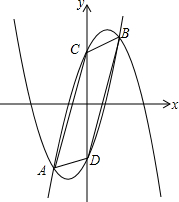 已知,如图,抛物线l1:y=-x2+2x+3与抛物线l2:y=x2+2x-3相交于点A,B,它们分别与y轴相交于C,D,其中点A的横坐标比点B的横坐标小.
已知,如图,抛物线l1:y=-x2+2x+3与抛物线l2:y=x2+2x-3相交于点A,B,它们分别与y轴相交于C,D,其中点A的横坐标比点B的横坐标小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com