
(本题满分6分)已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.

(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
AC=BD
【解析】
试题分析:(1)由于OA=OB,OC=OD,利用等边对等角易得∠A=∠B,∠OCD=∠ODC,而利用三角形外角性质可得∠OCD=∠A+∠AOC,∠ODC=∠BOD+∠B,从而可得∠A+∠AOC=∠BOD+∠B,再利用等量相减,差相等可得∠AOC=∠DOB;
(2)过O作OE⊥AB于E,利用垂径定理有AE=EB,CE=ED,于是AE-CE=BE-DE,即AC=BD.
 试题解析:
试题解析:
(1)∵AO=OB,OC=OD
∴∠A=∠B,∠OCD=∠ODC
∴∠OCA=∠ODC
∴△ACO=△ODB
∴∠AOC=∠DOB
(2)过O作OE⊥AB于E
∴AE=EB,CE=ED
∴AC=BD
考点:等边对等角,三角形外角性质,垂径定理


科目:初中数学 来源:2014-2015学年广东省八年级上学期期中数学试卷(解析版) 题型:选择题
下列说法中正确的是( )
A.已知 是三角形的三边,则
是三角形的三边,则
B.在直角三角形中,两边的平方和等于第三边的平方
C.在Rt△ 中,∠
中,∠ °,所以
°,所以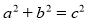
D.在Rt△ 中,∠
中,∠ °,所以
°,所以
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分12分)问题提出:平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考:设不在同一条直线上的三点A、B、C确定的圆为⊙O.
(1)当C、D在线段AB的同侧时,
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 ;
如图②,若点D在⊙O内,此时有∠ACB ∠ADB;
如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);

由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习:(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.

如图④,此时有 ,
如图⑤,此时有 ,
如图⑥,此时有 .
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件:
.
拓展延伸:(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图,AB是⊙O的直径,点C在⊙O上.

求作:CN⊥AB.
作法:①连接CA,CB;
②在 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN.则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片九年级上学期期中考试数学试卷(解析版) 题型:填空题
把球放在长方体纸盒内,球的一部分露出盒外,如图所示为正视图.已知EF=CD=16厘米,这个球的半径是 厘米.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片九年级上学期期中考试数学试卷(解析版) 题型:选择题
某公司在布置联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条。如图所示:在Rt△ABC中,AC=30cm,BC=40cm.依此裁下宽度为1cm的纸条,若使裁得的纸条的长都不小于5cm,则能裁得的纸条的张数是 ( )

A.24 B.25 C.26 D.27
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片七年级上学期期中考试数学试卷(解析版) 题型:填空题
已知代数式x ? 2y的值是 ,则代数式
,则代数式 ?2x + 4y ? 1的值是__________.
?2x + 4y ? 1的值是__________.
已知2a+3b=4,3a—2b=11,则10a+2b的值是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题12分)如图甲,在平面直角坐标系中,直线y= x+8分别交x轴、y轴于点A、B,⊙O的半径为2
x+8分别交x轴、y轴于点A、B,⊙O的半径为2 个单位长度.点P为直线y=
个单位长度.点P为直线y= x+8上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,且PC⊥PD.
x+8上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,且PC⊥PD.

(1)试说明四边形OCPD的形状(要有证明过程);
(2)求点P的坐标;
(3)如图乙,若直线y= x+b将⊙O的圆周分成两段弧长之比为1:3,请直接写出b的值
x+b将⊙O的圆周分成两段弧长之比为1:3,请直接写出b的值
(4)向右移动⊙O(圆心O始终保持在x轴上),试求出当⊙O与直线y= x+8有交点时圆心O的横坐标m的取值范围。
x+8有交点时圆心O的横坐标m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com