【题目】如图，菱形ABCD的周长为16 cm，∠BAD＝120°对角线AC，BD相交于点O，过点O作BC的垂线交BC于点E，交AD于点F，求EF长.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】我们知道，对任意一个正整数n都可以进行这样的分解：n=p
q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p
q是n的最佳分解，并规定：F（n）=
，例如12可以分解为1
12，2
6或3
4，因为12-1＞6-2＞4-3，所以3
4是最佳分解，所以F（n）=
。
（1）如果一个正整数
是另外一个正整数b的平方，我们称正整数a是完全平方数，求证：对任意一个完全平方数m，总有F（m）=1
（2）如果一个两位正整数t，t=10x+y （1≤x≤y≤9，x,y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们就称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC中，AB＝AC，∠BAC＝90°，∠1＝∠2，CE⊥BD交BD的延长线于点E，CE＝1，延长CE、BA交于点F．
（1）求证：△ADB≌△AFC；
（2）求BD的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=2
x2的图象如图所示，点O为坐标原点，点A在y轴的正半轴上，点B、C在函数图象上，四边形OBAC为菱形，且∠OBA=120°，则点C的坐标为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小王于上午8时从甲地出发去相距50千米的乙地. 右图中，折线
是表示小王离开甲地的时间
（时）与路程
（千米）之间的函数关系的图像.根据图像给出的信息，下列判断中，错误的是（ ）
A.小王11时到达乙地
B.小王在途中停了半小时
C.与8：009：30相比，小王在10：0011：00前进的速度较慢
D.出发后1小时，小王走的路程少于25千米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】右图是老北京城一些地点的分布示意图．在图中，分别以正东、正北方向为
轴、
轴的正方向建立平面直角坐标系，有如下四个结论：
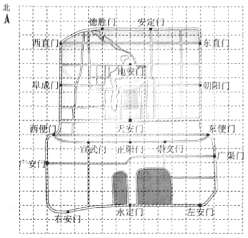
①当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（
，
）时，表示左安门的点的坐标为（5，）；
②当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（
，）时，表示左安门的点的坐标为（10，）；
③当表示天安门的点的坐标为（1，1），表示广安门的点的坐标为（
，
）时，表示左安门的点的坐标为（
，）；
④当表示天安门的点的坐标为（
，），表示广安门的点的坐标为（
，
）时，表示左安门的点的坐标为（
，）．
上述结论中，所有正确结论的序号是
A. ①②③ B. ②③④ C. ①④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
