
����Ŀ��2016����Լ���˻ᣬ�й�Ů�ŵĹ���������ƽ����ָ���£�ͨ���̿�ѵ����ȡ��������ھ���Ϊ�����⣬��ͼ����֪���ij���ODΪ18�ף�λ�������ߴ������ĸ߶�ABΪ2.43�ף�һ��Ավ�ڵ�O����������ӵ�O�����Ϸ�1.8��C������ǰ���ɳ������������������O��ˮƽ����OEΪ7��ʱ��������ߵ�G������ͼ��ʾ��ƽ��ֱ������ϵ��
��1���������������߶�Ϊ3.2��ʱ����������еĸ߶�y����λ���ף���ˮƽ����x����λ���ף��ĺ�����ϵʽ������Ҫ��д�Ա���x��ȡֵ��Χ����
��2���ڣ�1���������£��Է�������0.5�ĵ�F����һ��Ա��������������߶�Ϊ3.1�ף���������Ƿ���������ɹ�����ͨ������˵����
��3������Ա�����Ҫ���������ֲ����߽磬��������е����߶�h��ȡֵ��Χ�Ƕ��٣�������ѹ������û���磩

���𰸡���1��(1) ![]() ��2�����������ɹ�����3��h��
��2�����������ɹ�����3��h��![]()
�������������������1����������������ߵĶ���Ϊ��5��3����������������ߵĽ���ʽΪ![]() ����C��0��2�����뼴��. ��2����OD=15����OA=7.5, �߶Է�������0.5�ĵ�F����OF=8,��x��8�������ʽ���y��ֵ����2.7�Ƚϼ���. ��3������������ѽ���ʽ��Ϊy��(x��5)2��h����C��0��2�������
����C��0��2�����뼴��. ��2����OD=15����OA=7.5, �߶Է�������0.5�ĵ�F����OF=8,��x��8�������ʽ���y��ֵ����2.7�Ƚϼ���. ��3������������ѽ���ʽ��Ϊy��(x��5)2��h����C��0��2�������
a(��5)2��h��2�� ![]() ��Ҫ����������Ե�
��Ҫ����������Ե�![]() ʱ��
ʱ�� ![]() ��Ҫ���磬���Ե�
��Ҫ���磬���Ե�![]() ʱ��
ʱ�� ![]() ���ⲻ��ʽ�������h��ȡֵ��Χ.
���ⲻ��ʽ�������h��ȡֵ��Χ.
���������
(1) ![]()
(2) ��x��8ʱ�� ![]()
���������ɹ�
(3) ��y��(x��5)2��h
��C(0��2)����y��(x��5)2��h����
a(��5)2��h��2�� ![]()
��![]()
��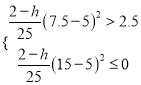 ���h��
���h��![]()


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ�ֽ���ȷ���ǣ�������
A.x2��4=��x+4����x��4��
B.x2+2x+1=x��x+2��+1
C.3mx��6my=3m��x��6y��
D.2x+4=2��x+2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������̳������Ƴ���ͬ���Żݷ������ڼ��̳��ۼƹ��ﳬ��100Ԫ��������100Ԫ�IJ��ְ�90%�շ��������̳��ۼƹ��ﳬ��50Ԫ��������50Ԫ�IJ��ְ�95%�շ�����С����ͬһ�̳��ۼƹ���xԪ������x��100��
��1��������������д�±�����λ��Ԫ����
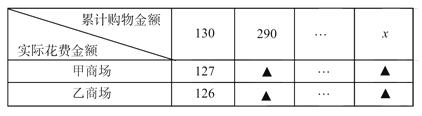
��2����xȡ��ֵʱ��С���ڼס������̳���ʵ�ʻ��ѽ����ͬ��
��3���������С���ۼƹ���Ľ��ѡ�ѽ��ٵ��̳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ÿ�ѧ��������ʾ�� 0.00000402= ________��3200000=____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ĵ�����Դ�ḻ�����ҵõ��˽ϺõĿ������õ���һ�ҹ��繫˾Ϊ�˹��������õ磬���÷ֶμƷѵķ����������ѣ����õ���x���ȣ�����Ӧ���y��Ԫ��֮��ĺ���ͼ����ͼ��ʾ��

��1�����õ���Ϊ100��ʱ��Ӧ����� Ԫ��
��2����x��100ʱ����y��x֮��ĺ�����ϵʽ��
��3�����õ���Ϊ260��ʱ��Ӧ����Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ���һ������ȱˮ�Ĺ��ң�Ϊ�˼�ǿ����Ľ�ˮ��ʶ��ij���ƶ���������ˮ�շѱ���ÿ��ÿ�µ���ˮ������6��ʱ��ˮ��Ϊÿ��2Ԫ������6��ʱ�������IJ��ְ�ÿ��3Ԫ�շѣ�����ij������5�·���ˮx�֣�Ӧ��ˮ��yԪ��
��1����0��x��6����д��y��x�ĺ�����ϵʽ��
��2����x��6����д��y��x�ĺ�����ϵʽ��
��3������û���������½�ˮ��27Ԫ����ô����¸û����˶��ٶ�ˮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֪ʶ��������������30��ǵ�ȫ�����dz߷���һ����������30���Ǻ���һ���60��������ƴ�ա��۲졢˼����̽������ֱ����������30������Ե�ֱ�DZߵ���б�ߵ�һ�롱������
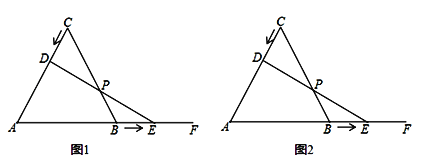
��ͼ���ȱ�������ABC�ı߳�Ϊ4cm����D�ӵ�C������CA��A�˶�����E��B������AB���ӳ���BF�����˶�����֪��D��E����ÿ��0.5cm���ٶ�ͬʱ��ʼ�˶����˶�������DE��BC�ཻ�ڵ�P�����˶�ʱ��Ϊx����
��1����ֱ��д��AD��������x�Ĵ���ʽ��ʾ��
��2������ADEΪֱ��������ʱ���˶�ʱ��Ϊ���룿
��2����֤�����˶�����������Pʼ��Ϊ�߶�DE���е���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���OBCD�е�������������O�ϣ���A���Ż�BD�ϵ�һ�����㣨�����B��D�غϣ���

��1����Բ��O����BAD�ڲ�����ABO+��ADO=60��ʱ����BOD= ��
��2����Բ��O����BAD�ڲ����ı���OBCDΪƽ���ı���ʱ������A�Ķ�����
��3����Բ��O����BAD�ⲿ���ı���OBCDΪƽ���ı���ʱ����ֱ��д����ABO����ADO��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ����ABC�У���BAC=90![]() ��AD��BC��D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬�ӳ�AM��BC�ڵ�N������DM�����н��ۣ���AE=AF����AM��EF����AF=DF����DF=DN��������ȷ�Ľ����У�������
��AD��BC��D����ABC��ƽ���߷ֱ�AC��AD��E��F���㣬MΪEF���е㣬�ӳ�AM��BC�ڵ�N������DM�����н��ۣ���AE=AF����AM��EF����AF=DF����DF=DN��������ȷ�Ľ����У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com