
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是优弧BD上的一个动点(不与点B、D重合).

(1)当圆心O在∠BAD内部,∠ABO+∠ADO=60°时,∠BOD= ;
(2)当圆心O在∠BAD内部,四边形OBCD为平行四边形时,求∠A的度数;
(3)当圆心O在∠BAD外部,四边形OBCD为平行四边形时,请直接写出∠ABO与∠ADO的数量关系.
【答案】(1)120 °;(2)60°;(3)60°.
【解析】试题分析:(1)连接OA,如图1,根据等腰三角形的性质得∠OAB=∠ABO,∠OAD=∠ADO,则∠OAB+∠OAD=∠ABO+∠ADO=60°,然后根据圆周角定理易得∠BOD=2∠BAD=120°;(2)根据平行四边形的性质得∠BOD=∠BCD,再根据圆周角定理得∠BOD=2∠A,则∠BCD=2∠A,然后根据圆内接四边形的性质由∠BCD+∠A=180°,易计算出∠A的度数;(3)讨论:当∠OAB比∠ODA小时,如图2,与(1)一样∠OAB=∠ABO,∠OAD=∠ADO,则∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,由(2)得∠BAD=60°,
所以∠ADO﹣∠ABO=60°;当∠OAB比∠ODA大时,用样方法得到∠ABO﹣∠ADO=60°.
试题解析:(1)连接OA,如图1,
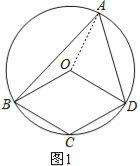
∵OA=OB,OA=OD, ∵∠OAB=∠ABO,∠OAD=∠ADO, ∴∠OAB+∠OAD=∠ABO+∠ADO=60°,即∠BAD=60°,
∴∠BOD=2∠BAD=120°;
(2)∵四边形OBCD为平行四边形, ∴∠BOD=∠BCD, ∵∠BOD=2∠A, ∴∠BCD=2∠A,
∵∠BCD+∠A=180°,即3∠A=180°, ∴∠A=60°;
(3)当∠OAB比∠ODA小时,如图2,

∵OA=OB,OA=OD, ∵∠OAB=∠ABO,∠OAD=∠ADO, ∴∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,
由(2)得∠BAD=60°, ∴∠ADO﹣∠ABO=60°; 当∠OAB比∠ODA大时,
同理可得∠ABO﹣∠ADO=60°, 综上所述,|∠ABO﹣∠ADO|=60°.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】2016年里约奥运会,中国女排的姑娘们在郎平教练指导下,通过刻苦训练,取得了世界冠军,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3.2米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)的函数关系式.(不要求写自变量x的取值范围).
(2)在(1)的条件下,对方距球网0.5米的点F处有一队员,他起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.
(3)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再因式分解:x4+4=(x4+4x2+4)-4x2=(x2+2)2-(2x)2=(x2-2x+2)(x2+2x+2),按照这种方法把多项式x4+64因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点 F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计(设每天的诵读时间为![]() 分钟),将调查统计的结果分为四个等级:Ⅰ级
分钟),将调查统计的结果分为四个等级:Ⅰ级![]() 、Ⅱ级
、Ⅱ级![]() 、Ⅲ级
、Ⅲ级![]() 、Ⅳ级
、Ⅳ级![]() .将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
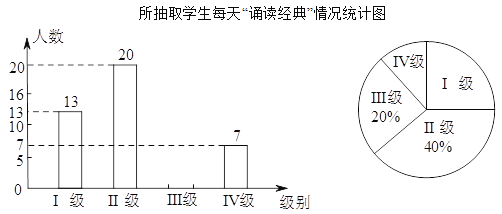
(![]() )请补全上面的条形图.
)请补全上面的条形图.
(![]() )所抽查学生“诵读经典”时间的中位数落在__________级.
)所抽查学生“诵读经典”时间的中位数落在__________级.
(![]() )如果该校共有
)如果该校共有![]() 名学生,请你估计该校平均每天“诵读经典”的时间不低于
名学生,请你估计该校平均每天“诵读经典”的时间不低于![]() 分钟的学生约有多少人?
分钟的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )

A. 勾股定理 B. 直径所对的圆周角是直角
C. 勾股定理的逆定理 D. 90°的圆周角所对的弦是直径
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com