如图，在△ABC中(BC>AC)，∠ACB=90°，点D在AB边上，DE⊥AC于点E
1) 若
=
，AE=2，求EC的长
2) 设点F在线段EC上，点G在射线CB上，以F，C，G为顶点的三角形与△EDC有一个锐角相等，FG交CD于点P，问：线段CP可能是△CFG的高线还是中线？或两者都有可能？请说明理由
芒果教辅达标测试卷系列答案科目：初中数学 来源： 题型：
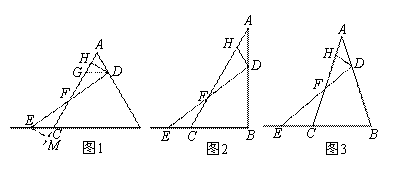
问题背景：已知在△ABC中，AB边上的动点D由A向B运动(与A，B不重合)，点E与点D同时出发，由点C沿BC的延长线方向运动(E不与C重合)，连结DE交AC于点F，点H是线段AF上一点
1) 初步尝试：如图1，若△ABC是等边三角形，DH⊥AC，且点D，E的运动速度相等，求证：HF=AH+CF
小王同学发现可以由
以下两种思路解决此问题：
思路一：过点D作D
G∥BC，交AC于点G，先证GH=AH，再证GF=CF，从而证得结论成立
思路二：过点E作EM⊥AC，交AC的延长线于点M，先证CM=AH，再证HF=MF，从而证得结论成立
请
你任选一种思路，完整地书写本小题的证明过程(如用两种方法作答，则以第一种方法评分)
2) 类比探究：如图2，若在△ABC中，∠ABC=90°，∠ADH=∠BAC=30°，且点D，E的运动速度之比是
：1，求
的值
3) 延伸拓展：如图3，若在△ABC中，AB=AC，∠ADH=∠BAC=36°，记
=m，且点D、E的运动速度相等，试用含m的代数式表示(直接写出结果，不必写解答过程)
查看答案和解析>>
科目：初中数学 来源： 题型：
设二次函数y1=a(x−x1)(x−x2)(a≠0，x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1，0)，若函数y=y2+y1的图象与x轴仅有一个交点，则(
)
A. a(x1−x2)=d B. a(x2−x1)=d C. a(x1−x2)2=d D. a(x1+x2)2=d
查看答案和解析>>
科目：初中数学 来源： 题型：
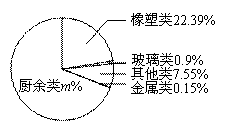
杭州市推行垃圾分类已经多年，但在厨余垃圾中除了厨余类垃圾还混杂着非厨余类垃
圾，如图是杭州市某一天收到的厨余垃圾的统计图
1) 试求出m的值
2) 杭州市那天共收到厨余垃圾约200吨，请计算其中混杂着的玻璃类垃圾的吨数
查看答案和解析>>
科目：初中数学 来源： 题型：
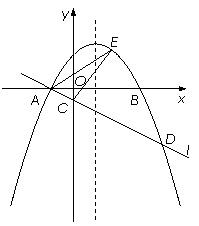
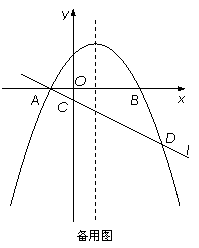
如图，在平面直角坐标系xOy中，抛物线y＝ax 2－2ax－3a（a＜0）与x轴交于A、B两点（点A在点B的左侧），经过点A的直线l：y＝kx＋b与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD＝4AC．
（1）直接写出点A的坐标，并求直线l的函数表达式（其中k、b用含a的式子表示）；
（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为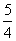 
，求a的值；
（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．
 |  | ||
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形，它的面积S可用公式
（
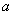是多边形内的格点数，
是多边形边界上的格点数）计算，这个公式称为“皮克定理”。现有一张方格纸共有200个格点，画有一个格点多边形，它的面积S=40.
（1）这个格点多边形边界上的格点数= （用含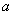的代数式表示）；
（2）设该格点多边形外的格点数为
，则
=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，
，
，
，
,
的长为
（B）
（D）
，
，则
________度.