
如图,在矩形ABCD中,AB的长度为a,BC的长度为b,其中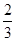 b<a<b.将此矩形纸片按下列顺序折叠,则C′D′的长度为 (用含a、b的代数式表示).
b<a<b.将此矩形纸片按下列顺序折叠,则C′D′的长度为 (用含a、b的代数式表示).

科目:初中数学 来源:2014中考名师推荐数学整体思想(解析版) 题型:选择题
解方程(x﹣1)2﹣5(x﹣1)+4=0时,我们可以将x﹣1看成一个整体,设x﹣1=y,则原方程可化为y2﹣5y+4=0,解得y1=1,y2=4.当y=1时,即x﹣1=1,解得x=2;当y=4时,即x﹣1=4,解得x=5,所以原方程的解为:x1=2,x2=5.则利用这种方法求得方程 (2x+5)2﹣4(2x+5)+3=0的解为( )
A.x1=1,x2=3
B.x1=﹣2,x2=3
C.x1=﹣3,x2=﹣1
D.x1=﹣1,x2=﹣2
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:解答题
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:


说明:方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
纸片利用率= ×100%
×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.
你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.
请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:选择题
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
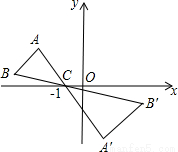
A. B.
B.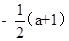 C.
C. D.
D.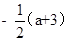
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的对称、平移与旋转(解析版) 题型:选择题
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3, ),点C的坐标为(
),点C的坐标为( ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形与坐标(解析版) 题型:选择题
对平面上任意一点(a,b),定义f,g两种变换:f(a,b)=(a,-b).如f(1,2)=(1,-2);g(a,b)=(b,a).如g(1,2)=(2,1).据此得g(f(5,-9))=( )
A.(5,-9)
B.(-9,-5)
C.(5,9)
D.(9,5)
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学二元一次方程组(解析版) 题型:选择题
利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
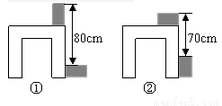
A.73cm B.74cm
C.75cm D.76cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com